练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．小张在做数学题时，发现了下面有趣的结果：
    3-2=1，
    8+7-6-5=4，
    15+14+13-12-11-10=9，
    24+23+22+21-20-19-18-17=16，
    …
    根据以上规律可知，第20行左起第一个数是（　　）
    A．360B．339C．440D．483

    分析 根据左起第一个数3，8，15，24…的变化规律得出第n行左起第一个数为（n+1）2-1，由此求出即可．

    解答 解：∵3=22-1，
    8=32-1，
    15=42-1，
    24=52-1，
    …
    ∴第20个式子左起第一个数是：212-1=440．
    故选：C．

    点评 此题主要考查了数字变化规律，根据已知得出数字的变与不变是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

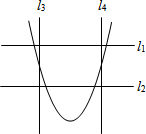    17．如图，水平线l1∥l2，铅垂线l3∥l4，l1⊥l3，若选择l1、l2其中一条当成x轴，且向右为正方向，再选择l3、l4其中一条当成y轴，且向上为正方向，并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象，则下列关于x、y轴的叙述，正确的是（　　）
    A．l1为x轴，l3为y轴B．l1为x轴，l4为y轴C．l2为x轴，l3为y轴D．l2为x轴，l4为y轴

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

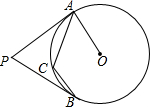    18．如图，PA，PB分别与⊙O相切于A、B，点C在劣弧AB上（不与A，B重合），若∠APB=70°，则∠ACB=（　　）
    A．140°B．145°C．110°D．125°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

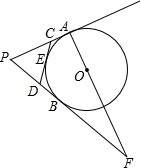    15．如图，PA，PB切⊙O于A，B两点，CD切⊙O于点E，交PA，PB于点C，D，连接AO并延长交PB的延长线于点F．若⊙O的半径为r，△PCD的周长等于3r，则$\frac{OA}{OF}$的值是$\frac{5}{13}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．兴华初中准备购买10副某种品牌的乒乓球拍，每幅球拍配x（x≥2）个乒乓球，该校附近A，B两家超市都有这种品牌的乒乓球拍和乒乓球出售，且每副球拍的标价均为40元，每个乒乓球的标价为4元，目前两家超市同时在做促销活动：
    A超市：所有商品均打九折（按标价的90%）销售；
    B超市：买一副乒乓球拍送2个乒乓球．
    设在A超市购买乒乓球拍和乒乓球的费用为yA（元），在B超市购买乒乓球拍和乒乓球的费用为yB（元）．请解答下列问题：
    （1）分别写出yA、yB与x之间的关系式；
    （2）若该活动中心只在一家超市购买，你认为在哪家超市购买更划算？
    （3）若每副球拍配15个乒乓球，请你帮助该活动中心设计出最省钱的购买方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

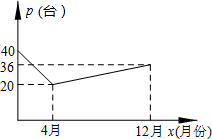    12．由于国家重点扶持节能环保产业，某种节能产品的销售市场逐渐回暖，某经销商销售这种产品，年初与生产厂家签订了一份进货合同，约定一年内进价为0.1万元/台．若一年内该产品的售价y（万元/台）与月份x（1≤x≤12且为整数）满足关系式：y=$\left\{\begin{array}{l}-0.05x+0.4（1≤x＜4）\\ 0.2（4≤x≤12\end{array}）$，一年后，发现这一年来实际每月的销售量p（台）与月份x之间存在如图所示的变化趋势．
    （1）求实际每月的销售量p（台）与月份x之间的函数表达式；
    （2）全年中哪个月份的实际销售利润w最高，最高为多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，在平面直角坐标系中，矩形OCDE的两个顶点分别是C（3，0），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴x=1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t s．
    （1）填空：点A的坐标为（1，4）；抛物线的解析式为y=-x2+2x+3．
    （2）在图1中，若点P在线段OC上从点O向点C以每秒1个单位的速度运动，同时，点Q在线段CE上从点C向点E以每秒2个单位的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？
    （3）在图2中，若点P在对称轴x=1上从点A开始向点B以每秒1个单位的速度运动，过点P作PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？

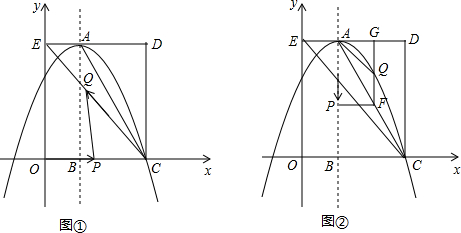
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

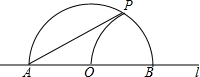    16．如图，直线l上一点O，以O为圆心，任意长为半径画半圆，交l于A、B两点，再以B为圆心，OB的长为半径画弧交半圆于P，连AP，则sin∠PAB的值等于$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

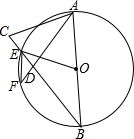    17．如图，等腰三角形ABC中，BA=BC，以AB为直径作圆，交BC于点E，圆心为O．在EB上截取ED=EC，连接AD并延长，交⊙O于点F，连接OE、EF．
    （1）试判断△ACD的形状，并说明理由；
    （2）求证：∠ADE=∠OEF．

    查看答案和解析>>

    同步练习册答案