
分析 (1)根据购买费用=单价×数量建立关系就可以表示出yA、yB的解析式;
(2)分三种情况进行讨论:当yA=yB时,当yA>yB时,当yA<yB时,分别求出购买划算的方案;
(3)分两种情况进行讨论计算求出需要的费用,再进行比较就可以求出结论.
解答 解:(1)由题意,得yA=(10×40+40x)×0.9=36x+360,yB=10×40+4(x-20)=4x+320.
(2)当yA=yB时,3.6x+360=4x+320,得x=100;
当yA>yB时,3.6x+360>4x+320,得x<100;
当yA<yB时,3.6x+360<4x+320,得x>100,
∴当2≤x<100时,到B超市购买划算,
当x=100时,两家超市一样划算,
当x>100时在A超市购买划算.
(3)由题意,知x=15×10=150>100,
∴选择A超市,yA=3.6×150+360=900(元);
如果先选择B超市购买10副乒乓球拍,送20个乒乓球,费用为400元,然后在A超市购买剩下的乒乓球,费用为(10×15-20)×4×0.9=468(元),共需费用868元.
∵868<900,
∴最佳方案是先选择在B超市购买10副乒乓球拍,然后在A超市购买130个乒乓球.
点评 本题考查了一次函数的解析式的运用,分类讨论的数学思想的运用,方案设计的运用,解答时求出函数的解析式是关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
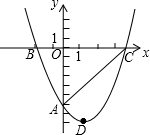 如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.
如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 360 | B. | 339 | C. | 440 | D. | 483 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25 | B. | -25 | C. | $\frac{1}{25}$ | D. | -$\frac{1}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\root{3}{-8}$ | C. | $\sqrt{4}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
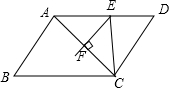 如图,已知AD∥BC,AB∥CD,AB=4,BC=6,EF是AC的垂直平分线,分别交AD、AC于E、F,连结CE,则△CDE的周长是10.
如图,已知AD∥BC,AB∥CD,AB=4,BC=6,EF是AC的垂直平分线,分别交AD、AC于E、F,连结CE,则△CDE的周长是10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com