
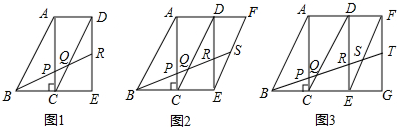
分析 (1)首先证明△BCQ∽△BES,从而可求得CQ=$\frac{1}{4}EF$,DQ=$\frac{3}{4}$EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2;
(2)由AC∥DE∥GF,可知:△BPC∽△BER∽BTG,能够求得:AP:DR:FT=5:4:3,然后再证明△BAP∽△QDR∽△SFT.求得BP:QR:ST=AP:DR:FT=5:4:3,因为BP:QR:RT=5:4:5,所以可求得:BP:PQ:QR:RS:ST=5:1:4:2:3.
解答 解:(1)∵四个直角三角形是全等三角形,
∴AB=EF=CD,AB∥EF∥CD,BC=CE,AC∥DE,
∴BP:PR=BC:CE=1,
∵CD∥EF,
∴△BCQ∽△BES.
又∵BC=CE
∴CQ=$\frac{1}{2}SE$=$\frac{1}{4}EF$,
∴DQ=$\frac{3}{4}EF$
∵AB∥CD,
∴∠ABP=∠DQR.
又∵∠BAP=∠QDR,
∴△BAP∽△QDR.
∴BP:QR=4:3.
∴BP:PQ:QR=4:1:3,
∵DQ∥SE,
∴QR:RS=DQ:SE=3:2,
∴BP:PQ:QR:RS=4:1:3:2.
故答案为:4:1:3:2;
(2)∵五个直角三角形是全等直角三角形
∴AB=CD=EF,AB∥CD∥EF,AC=DE=GF,AC∥DE∥GF,
BC=CE=EG,
∴BP=PR=RT,
∵AC∥DE∥GF,
∴△BPC∽△BER∽BTG,
∴PC=$\frac{1}{3}TG$=$\frac{1}{6}FG$,RE=$\frac{2}{3}TG$=$\frac{1}{3}$FG,
∴AP=$\frac{5}{6}FG$,DR=$\frac{2}{3}FG$,FT=$\frac{1}{2}FG$
∴AP:DR:FT=5:4:3.
∵AC∥DE∥GF,
∴∠BPA=∠QRD=∠STF.
又∵∠BAP=∠QDR=∠SFT,
∴△BAP∽△QDR∽△SFT.
∴BP:QR:ST=AP:DR:FT=5:4:3.
又∵BP:QR:RT=5:4:5,
∴BP:PQ:QR:RS:ST=5:(5-4):4:(5-3):3=5:1:4:2:3.
故答案为:5:1:4:2:3.
点评 本题主要考查的是相似三角形的判定和性质,找出图中的相似三角形,求得相应线段之间的比例关系是解题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
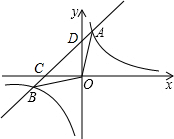 已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.
已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
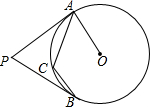 如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )| A. | 140° | B. | 145° | C. | 110° | D. | 125° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
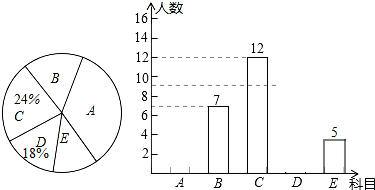
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 等级 | 票价(元/张) |
| A | 150 |
| B | 300 |
| C | 500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com