
分析 首先根据分式混合运算的运算顺序,先计算小括号里面的,再计算除法,把原式进行化简,然后把a=1,b=2代入化简后的算式,求出算式($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$的值是多少即可.
解答 解:($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$
=($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{a-b}{{a}^{2}{-b}^{2}}$)÷$\frac{b}{b-a}$
=$\frac{b}{{a}^{2}{-b}^{2}}÷\frac{b}{b-a}$
=-$\frac{1}{a+b}$,
当a=1,b=2时,
-$\frac{1}{a+b}$=-$\frac{1}{1+2}=-\frac{1}{3}$.
点评 此题主要考查了分式的化简求值问题,注意化简时不能跨度太大,而缺少必要的步骤,解答此题的关键是要明确:代入求值时,有直接代入法,整体代入法等常用方法.解题时可根据题目的具体条件选择合适的方法.当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式都有意义,且除数不能为0.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
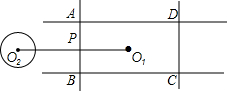 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )| A. | 18次 | B. | 12次 | C. | 8次 | D. | 4次 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
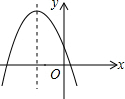 抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )| A. | 一、三象限 | B. | 一、二象限 | C. | 二、三象限 | D. | 二、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com