
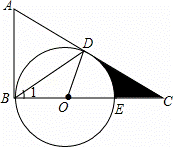
)如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
考点: 切线的判定;扇形面积的计算.
专题: 几何综合题;压轴题.
分析: (1)由OD=OB得∠1=∠ODB,则根据三角形外角性质得∠DOC=∠1+∠ODB=2∠1,而∠A=2∠1,所以∠DOC=∠A,由于∠A+∠C=90°,所以∠DOC+∠C=90°,则可根据切线的判定定理得到AC是⊙O的切线;
(2)解:由∠A=60°得到∠C=30°,∠DOC=60°,根据含30度的直角三角形三边的关系得CD=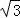 OD=2
OD=2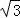 ,然后利用阴影部分的面积=S△COD﹣S扇形DOE
,然后利用阴影部分的面积=S△COD﹣S扇形DOE
和扇形的面积公式求解.
解答: (1)证明:∵OD=OB,
∴∠1=∠ODB,
∴∠DOC=∠1+∠ODB=2∠1,
而∠A=2∠1,
∴∠DOC=∠A,
∵∠A+∠C=90°,
∴∠DOC+∠C=90°,
∴OD⊥DC,
∴AC是⊙O的切线;
(2)解:∵∠A=60°,
∴∠C=30°,∠DOC=60°,
在Rt△DOC中,OD=2,
∴CD=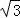 OD=2
OD=2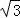 ,
,
∴阴影部分的面积=S△COD﹣S扇形DOE
=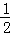 ×2×2
×2×2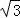 ﹣
﹣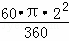
=2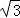 ﹣
﹣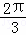 .
.
点评: 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了扇形面积的计算.


科目:初中数学 来源: 题型:
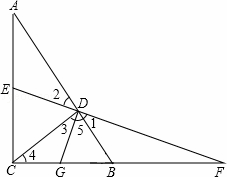
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.
(1)求证:FD2=FB•FC;
(2)若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com