
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.
(1)求证:FD2=FB•FC;
(2)若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由.
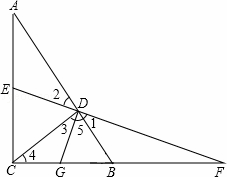
考点: 相似三角形的判定与性质;直角三角形斜边上的中线.
专题: 综合题.
分析: (1)要求证:FD2=FB•FC,只要证明△FBD∽△FDC,从而转化为证明∠FDC=∠FBD;
(2)要证DG⊥EF,只要证明∠5+∠1=90°,转化为证明∠3=∠4即可.
解答: (1)证明:∵E是Rt△ACD斜边中点,
∴DE=EA,
∴∠A=∠2,(1分)
∵∠1=∠2,
∴∠1=∠A,(2分)
∵∠FDC=∠CDB+∠1=90°+∠1,∠FBD=∠ACB+∠A=90°+∠A,
∴∠FDC=∠FBD,
∵∠F是公共角,
∴△FBD∽△FDC.(4分)
∴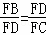 .
.
∴FD2=FB•FC.(6分)
(2)GD⊥EF.(7分)
理由如下:
∵DG是Rt△CDB斜边上的中线,
∴DG=GC.
∴∠3=∠4.
由(1)得∵△FBD∽△FDC,
∴∠4=∠1,
∴∠3=∠1.(9分)
∵∠3+∠5=90°,
∴∠5+∠1=90°.
∴DG⊥EF.(10分)
点评: 证明线段的积相等可以转化为证明三角形相似,证明两直线垂直转化为证明形成的角是直角.


科目:初中数学 来源: 题型:
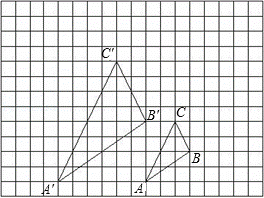
如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形顶点上.
(1)画出位似中心点O;
(2)△ABC与△A′B′C′的位似比为 1:2 ;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似为1:2.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,上体育课,九年级三班的甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是( )
A. 4米 B. 5米 C. 6米 D. 7米
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
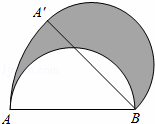
A. π B. 2π C.  D. 4π
D. 4π
查看答案和解析>>
科目:初中数学 来源: 题型:
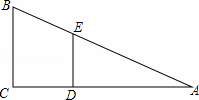
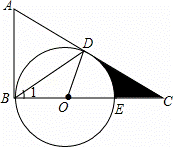
)如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
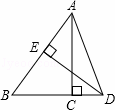
如图,在Rt△ABC中,∠ACB=90°,BC=3,AC= ,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
A. 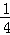 B.
B. 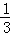 C.
C.  D.
D. 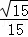
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com