
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:选择题
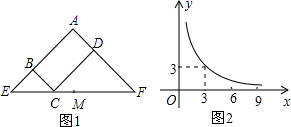
| A. | 当x=3时,EC<EM | B. | 当y=9时,EC>EM | ||
| C. | 当x增大时,EC•CF的值不变 | D. | 当y增大时,BE•DF的值增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
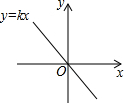 已知函数y=kx的图象如图所示,则对一元二次方程x2+x+k-1=0根的情况,说法正确的是( )
已知函数y=kx的图象如图所示,则对一元二次方程x2+x+k-1=0根的情况,说法正确的是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
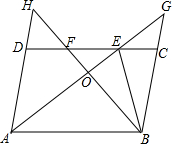 如图,在?ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
如图,在?ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )| A. | BO=OH | B. | DF=CE | C. | DH=CG | D. | AB=AE |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780-1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845-1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780-1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845-1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )| A. | 5 | B. | 4 | C. | $3+\sqrt{2}$ | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
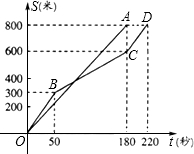 在今年我县初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小英和小西所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,如图,下列说法正确的是( )
在今年我县初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小英和小西所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,如图,下列说法正确的是( )| A. | 小英的速度随时间的增大而增大 | |
| B. | 小西的平均速度比小英的平均速度大 | |
| C. | 在起跑后180秒时,两人相遇 | |
| D. | 在起跑后50秒时,小西在小英的前面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com