
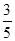 ,求⊙O的半径.
,求⊙O的半径.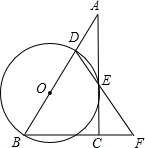
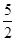 .
.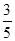 ,在Rt△ABC和Rt△AOC中分别应用锐角三角函数定义求解.
,在Rt△ABC和Rt△AOC中分别应用锐角三角函数定义求解.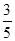 ,∴可设BC=3x, AB=5x.
,∴可设BC=3x, AB=5x.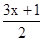 , AO=AB﹣OB=
, AO=AB﹣OB=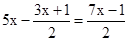 .]
.]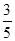 ,
,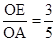 ,即
,即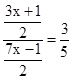 ,解得:x=
,解得:x=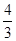 .
.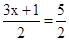 .
.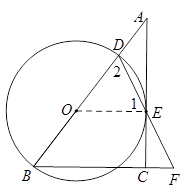


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源:不详 题型:单选题
| A.外离 | B.外切 | C.相交 | D.内切 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
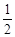 BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com