
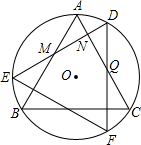
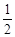 BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.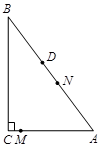
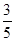 ;(2)t=1或t=2.
;(2)t=1或t=2. ,∴ 16
,∴ 16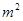 +
+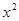 =
= . 解之得 x=3m.
. 解之得 x=3m.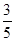 .
.
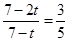 ,t=2,符合题意;
,t=2,符合题意;  ,t=-14,舍去;
,t=-14,舍去; 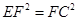 .
.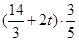 ,EF=FC=
,EF=FC=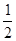 EC=
EC=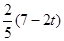 ,
,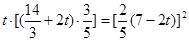 ,整理得
,整理得 ,解之得 t=1,t=-14(舍去) .
,解之得 t=1,t=-14(舍去) .


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源:不详 题型:解答题
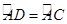 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.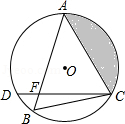
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
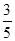 ,求⊙O的半径.
,求⊙O的半径.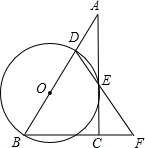
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com