练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
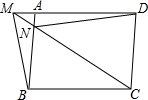
    14．如图，已知：?ABCD，M是DA延长线上一点，连接MB，MC，且MC交AB于点N，连接DN，求证：S△BMN=S△AND．

    分析 由平行四边形的性质得出△BCM的面积=$\frac{1}{2}$?ABCD的面积，△CDN的面积=$\frac{1}{2}$?ABCD的面积，得出△BMN的面积+△BCN的面积=△BCN的面积+△AND的面积，即可得出结论．

    解答 证明：∵四边形ABCD是平行四边形，
    ∴DM∥BC，AB∥CD，
    ∴△BCM的面积=$\frac{1}{2}$?ABCD的面积，△CDN的面积=$\frac{1}{2}$?ABCD的面积，
    ∴△BCN的面积+△AND的面积=$\frac{1}{2}$?ABCD的面积，
    ∴△BMN的面积+△BCN的面积=△BCN的面积+△AND的面积，
    ∴S△BMN=S△AND．

    点评 本题考查了平行四边形的性质、三角形与平行四边形的面积关系；熟记平行四边形的性质，理解三角形与平行四边形的面积关系是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．观察下列算式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，…通过观察，写出22015的末位数是8，类比这个探索过程，猜测32014末位数是9，20172017的末位数是7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

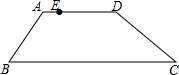    5．如图，四边形ABCD是梯形，AD∥BC，E为AD上任意一点，∠B+∠C=90°，请先将AB向右平移，使点A与点E重合，交BC于点F，再将CD向作平移，使点D与点E重合，交BC于点G，画出平移后的图形，并判断△EFG的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，?ABCD与?ABEF中，BC=BE，∠ABC=∠ABE，求证：四边形EFDC是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．分解因式：1-a2+ab-$\frac{1}{4}$b2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图所示，在△ABC中，∠ACB=90°，高CD和角平分线AE交于点F，求证：CF=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

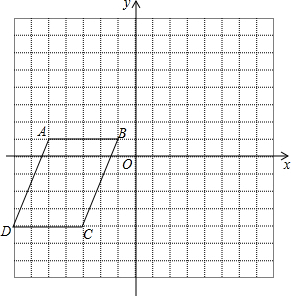    6．四边形ABCD的顶点坐标分别为A（-5，-1），B（-1，-1），C（-3，-4），D（-7，-4），将四边形ABCD先向上平移5个单位长度，再向右平移8个单位长度．
    （1）请直接写出第二次平移后四边形A′B′C′D′各个对应点的坐标和在平面直角坐标系中画出两个四边形．
    （2）如果四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的，请指出这一平移方向和平移距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

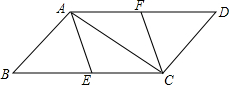    3．如图，?ABCD中，E，F分别为BC，AD的中点．
    （1）求证：四边形AECF为平行四边形；
    （2）若添加条件AB⊥AC，四边形AECF是什么四边形？说明理由；
    （3）若在（2）的基础上，在添加条件AB=AC，四边形AECF是什么四边形？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）（$\sqrt{3}$+$\sqrt{6}$）2
    （2）$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$
    （3）$\sqrt{18}+{（\sqrt{2}+1）^{-1}}+{（-2）^{-2}}$
    （4）$\frac{2}{3}\sqrt{3\frac{3}{4}}×（-9\sqrt{45}）$．

    查看答案和解析>>

    同步练习册答案