
分析 (1)由甲在长为4800米的直线街道上匀速巡逻,甲从a地出发向b地行走,80分钟巡逻完,根据速度=路程÷时间可得甲的速度;先求出乙以甲的$\frac{4}{3}$倍速度向a地行走一半路程所用的时间,再用甲走一半路程所用的时间40分钟减去乙走一半路程所用的时间即可得到乙中途休息的时间;
(2)甲与a地的距离y1=甲的速度×甲行时间;求乙与a地的距离y2与x的解析式需分三种情况进行讨论:①0≤x≤30;②30<x≤40;③40<x≤100;
(3)两人保持联系时,两人的距离不超过100米,分三种情况0≤x≤30;30<x≤40;40<x≤100建立不等式,解不等式即可.
解答 解:(1)甲的速度是:4800÷80=60(米/分);
乙走一半路程所用的时间:2400÷(60×$\frac{4}{3}$)=30(分钟),
乙中途休息了:40-30=10(分钟).
答:甲的速度是60米/分,乙中途休息了10分钟;
(2)y1=60x;
当0≤x≤30时,y2=4800-80x,
当30<x≤40时,y2=2400,
当40<x≤100时,y2=2400-40(x-40)=4000-40x,
即y2=$\left\{\begin{array}{l}{4800-80x(0≤x≤30)}\\{2400(30<x≤40)}\\{4000-40x(40<x≤100)}\end{array}\right.$;
(3)当0≤x≤30时,由4800-80x-60x≤100,解得x≥33$\frac{4}{7}$,不合题意舍去;
当30<x≤40时,由2400-60x≤100,解得x≥38$\frac{1}{3}$,即38$\frac{1}{3}$≤x≤40;
当40<x≤100时,由60x-(4000-40x)≤100,解得x≤41,即40<x≤41.
综上所述,可得两人保持联系的时间范围是38$\frac{1}{3}$≤x≤41.
点评 本题考查了一次函数的应用,一元一次不等式的应用,路程、速度、时间关系的应用,分类讨论思想的应用,求出y1,y2与x的函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
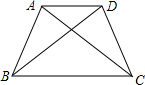 已知AB=CD,AC=BD,说明AD∥BC.
已知AB=CD,AC=BD,说明AD∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
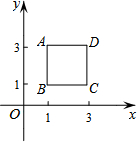 规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为(-1,-3),如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为(-3,-3).
规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为(-1,-3),如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为(-3,-3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是$\sqrt{3}$+1.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是$\sqrt{3}$+1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com