
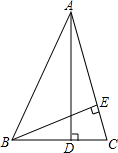
 已知:△ABC中,AD⊥BC,BE⊥AC交AD于点F,若∠BAC=45°,CD=1,BD=$\frac{3}{2}$,求AD的长.
已知:△ABC中,AD⊥BC,BE⊥AC交AD于点F,若∠BAC=45°,CD=1,BD=$\frac{3}{2}$,求AD的长. 分析 由∠BAC=45°可以得到BE=AE,再根据已知条件可以证明△AFE≌△BCE,可以得到AF=BC=10,而∠FBD=∠DAC,又∠BDF=∠ADC=90°,由此可以证明△BDF∽△ADC,所以FD:DC=BD:AD,设FD长为x,则可建立关于x的方程,解方程即可求出FD,AD的长.
解答 解:AD与BE相交于F,如图: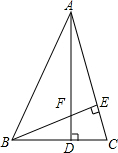
∵∠BAC=45°
∴BE=AE,
∵∠C+∠EBC=90°,∠C+∠EAF=90°,
∴∠EAF=∠EBC,
在△AFE与△BCE中,
$\left\{\begin{array}{l}{∠EAF=∠EBC}\\{BE=AE}\\{∠FEA=∠CEB=90°}\end{array}\right.$,
∴△AFE≌△BCE(ASA)
∴AF=BC=BD+DC=$\frac{5}{2}$,∠FBD=∠DAC,
又∵∠BDF=∠ADC=90°
∴△BDF∽△ADC
∴FD:DC=BD:AD
设FD长为x,则x:1=$\frac{3}{2}$:(x+$\frac{5}{2}$),解得x=0.5,即FD=0.5
∴AD=AF+FD=2.5+0.5=3.
答:AD长为3
点评 本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
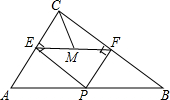 如图,已知在△ABC中,AC=3,BC=4,AB=5,点P是AB上 (不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连结EF,M为EF的中点.
如图,已知在△ABC中,AC=3,BC=4,AB=5,点P是AB上 (不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连结EF,M为EF的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
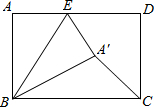 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )| A. | 3或4$\sqrt{2}$ | B. | 4或3$\sqrt{2}$ | C. | 3或4 | D. | 3$\sqrt{2}$或4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
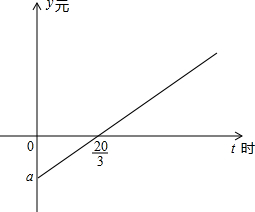 某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.
某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com