
 受台风影响,一棵大树从B处被折断,树的顶部落在离树根底部C相距4米的A处,测得∠CAB=60°,那么这棵树折断前高为14.9米$(结果保留一位小数,\sqrt{3}≈1.73)$.
受台风影响,一棵大树从B处被折断,树的顶部落在离树根底部C相距4米的A处,测得∠CAB=60°,那么这棵树折断前高为14.9米$(结果保留一位小数,\sqrt{3}≈1.73)$.  考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11+$\frac{11\sqrt{3}}{2}$ | B. | 11+$\frac{11\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$ | ||
| C. | 11+$\frac{11\sqrt{3}}{2}$或11-$\frac{11\sqrt{3}}{2}$ | D. | 11-$\frac{11\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$的算术平方根是$\sqrt{3}$ | B. | ±$\frac{3}{4}$是$\frac{9}{16}$的算术平方根 | ||
| C. | -8的立方根是2 | D. | 0没有平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
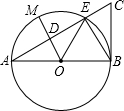 如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$的中点,OM交AC于点D,∠BOE=60°,cosC=$\frac{1}{2}$,BC=2$\sqrt{3}$,则MD的长度为( )
如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$的中点,OM交AC于点D,∠BOE=60°,cosC=$\frac{1}{2}$,BC=2$\sqrt{3}$,则MD的长度为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com