Question

20．在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB=5，BC=6，则CE+CF的值为（　　）

• A． 11+$\frac{11\sqrt{3}}{2}$
• B． 11+$\frac{11\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$
• C． 11+$\frac{11\sqrt{3}}{2}$或11-$\frac{11\sqrt{3}}{2}$
• D． 11-$\frac{11\sqrt{3}}{2}$

Answer 1

分析 根据平行四边形面积求出AE和AF，有两种情况，求出BE、DF的值，求出CE和CF的值，相加即可得出答案．

解答 解：∵四边形ABCD是平行四边形，
∴AB=CD=5，BC=AD=6，
①如图：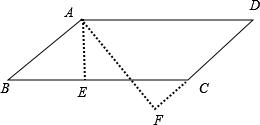

由平行四边形面积公式得：BC×AE=CD×AF=15，
求出AE=$\frac{5}{2}$，AF=3，
在Rt△ABE和Rt△ADF中，由勾股定理得：AB²=AE²+BE²，
把AB=5，AE=$\frac{5}{2}$代入求出BE=$\frac{5}{2}$$\sqrt{3}$，
同理DF=3$\sqrt{3}$＞5，即F在DC的延长线上（如上图），
∴CE=6-$\frac{5}{2}$$\sqrt{3}$，CF=3$\sqrt{3}$-5，
即CE+CF=1+$\frac{\sqrt{3}}{2}$，
②如图：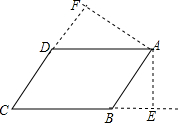

∵AB=5，AE=$\frac{5}{2}$，在△ABE中，由勾股定理得：BE=$\frac{5}{2}$$\sqrt{3}$，
同理DF=3$\sqrt{3}$，由①知：CE=6+$\frac{5}{2}$$\sqrt{3}$，CF=3$\sqrt{3}$+5，
∴CE+CF=11+$\frac{11}{2}$$\sqrt{3}$．
故选：B．

点评 此题考查了平行四边形的性质以及勾股定理．此题难度适中，注意掌握数形结合思想与分类讨论思想的应用．