
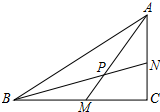
 如图,在直角△ABC的两直角边AC、BC上有两点M、N,AN=CM,AC=BM,AM与BN相交于P,则∠BPM=45°.
如图,在直角△ABC的两直角边AC、BC上有两点M、N,AN=CM,AC=BM,AM与BN相交于P,则∠BPM=45°. 分析 过点M作ME∥AN,使ME=AN,连NE,BE,得出四边形AMEN为平行四边形,再通过求证△BEM≌△AMC,可得出△BEN为等腰直角三角形,进而再利用平行线的性质可得出结论.
解答 证明:如图所示: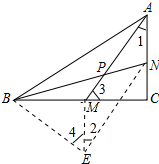 过M作ME∥AN,使ME=AN,连接NE、BE,
过M作ME∥AN,使ME=AN,连接NE、BE,
则四边形AMEN为平行四边形,
∴NE=AM,∠1=∠2,ME⊥BC,
∴∠BME=90°,
∵AN=CM,
∴ME=CM,
在△BEM和△AMC中,
$\left\{\begin{array}{l}{BM=AC}&{\;}\\{∠BME=∠ACB=90°}&{\;}\\{ME=CM}&{\;}\end{array}\right.$,
∴△BEM≌△AMC(SAS),
∴BE=AM,∠4=∠3,
∴BE=NE,
∵∠1+∠3=90°,
∴∠2+∠4=90°,
∴∠BEN=90°,
∴△BEN为等腰直角三角形,
∴∠BNE=45°,
∵AM∥NE,
∴∠BPM=∠BNE=45°.
点评 本题主要考查平行四边形的判定及性质、等腰直角三角形的性质及全等三角形的判定及性质;通过作辅助线构造三角形全等是解决问题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:填空题
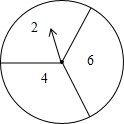 把一个转盘平均分成三等份,依次标上数字2、4、6,小红自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字除以2所得的商记作y,以x,y,5的边长的三条线段,能够构成三角形的概率为$\frac{4}{9}$.
把一个转盘平均分成三等份,依次标上数字2、4、6,小红自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字除以2所得的商记作y,以x,y,5的边长的三条线段,能够构成三角形的概率为$\frac{4}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组对边平行且另一组对边相等的四边形是平行四边形 | |
| B. | 至少有两个角是直角的四边形是矩形 | |
| C. | 有一组邻边相等的平行四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11+$\frac{11\sqrt{3}}{2}$ | B. | 11+$\frac{11\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$ | ||
| C. | 11+$\frac{11\sqrt{3}}{2}$或11-$\frac{11\sqrt{3}}{2}$ | D. | 11-$\frac{11\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com