
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
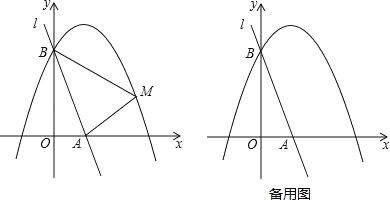
【答案】(1)y=﹣x2+2x+3;(2)S=-m2+m,最大值为;(3)①(,),②45°.
【解析】
试题分析:(1)先求出B点坐标,再把B点坐标代入即可求二次函数解析式;(2)根据M的位置可确定0<m<3,过点M作ME⊥y轴于点E,交AB于点D,可设M的坐标为(m,﹣m2+2m+3),用含m的式子表示DM,然后求出S与m的函数关系式,最大值也可求出.(3)①把m=代入二次函数解析式,可求出M′的坐标,②过点M′作直线l1∥l′,过点B作BF⊥l1于点F,则BF=d1+d2,当BF最大时可求出旋转角.
试题解析: (1)令x=0代入y=﹣3x+3,∴y=3,∴B(0,3),把B(0,3)代入y=ax2﹣2ax+a+4,∴3=a+4,
∴a=﹣1,∴二次函数解析式为:y=﹣x2+2x+3;(2)当y=0时,0=﹣x2+2x+3,∴x=﹣1或3,∴抛物线与x轴的交点横坐标为﹣1和3,∴0<m<3,过点M作ME⊥y轴于点E,交AB于点D,由题意知:M的坐标为(m,﹣m2+2m+3),∴D的纵坐标为:﹣m2+2m+3,∴把y=﹣m2+2m+3代入y=﹣3x+3,∴x=![]() ,∴D的坐标为(
,∴D的坐标为(![]() ,﹣m2+2m+3),∴DM=m﹣
,﹣m2+2m+3),∴DM=m﹣![]() =
=![]() ,∴S=DMOB=×
,∴S=DMOB=×![]() ×3=-m2+m=-(m-)2+,S最大值为;(3)①由(2)可知:M′的坐标为(,);②过点M′作直线l1∥l′,过点B作BF⊥l1于点F根据题意知:d1+d2=BF,∵∠BFM′=90°,∴点F在以BM′为直径的圆上,设直线AM′与该圆相交于点H,∵点C在线段BM′上,∴F在优弧BM′H上,∴当F与M′重合时,BF可取得最大值,此时BM′⊥l1,∵A(1,0),B(0,3),M′(,),∴由勾股定理可求得:AB=,M′B=
×3=-m2+m=-(m-)2+,S最大值为;(3)①由(2)可知:M′的坐标为(,);②过点M′作直线l1∥l′,过点B作BF⊥l1于点F根据题意知:d1+d2=BF,∵∠BFM′=90°,∴点F在以BM′为直径的圆上,设直线AM′与该圆相交于点H,∵点C在线段BM′上,∴F在优弧BM′H上,∴当F与M′重合时,BF可取得最大值,此时BM′⊥l1,∵A(1,0),B(0,3),M′(,),∴由勾股定理可求得:AB=,M′B=![]() ,M′A=
,M′A=![]() ,过点M′作M′G⊥AB于点G,设BG=x,∴由勾股定理可得:M′B2﹣BG2=M′A2﹣AG2,∴ ﹣(﹣x)2=﹣x2,∴x=
,过点M′作M′G⊥AB于点G,设BG=x,∴由勾股定理可得:M′B2﹣BG2=M′A2﹣AG2,∴ ﹣(﹣x)2=﹣x2,∴x=![]() ,
,
cos∠M′BG=![]() ,∵l1∥l′,∴∠BCA=90°,∠BAC=45°.
,∵l1∥l′,∴∠BCA=90°,∠BAC=45°.




科目:初中数学 来源: 题型:
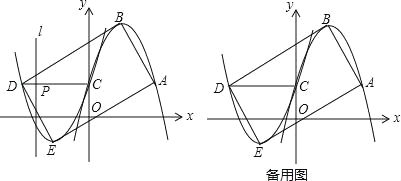
【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2,点A,B的对应点分别为点D,E.
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
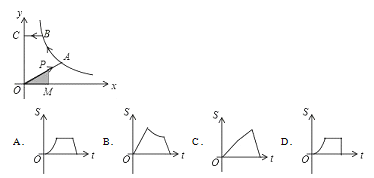
【题目】如图,已知A,B是反比例函数y=![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=(x-3)-1可以由抛物线y=x+1平移得到,则下列平移方法正确的是( )
A.先向左平移3个单位,再向上平移2个单位
B.先向左平移3个单位,再向下平移2个单位
C.先向右平移3个单位,再向上平移2个单位
D.先向右平移3个单位,再向下平移2个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果(7,3)表示电影票上“7排3号”,那么3排7号就表示为( )
A. (7,3) B. (3,7)
C. (-7,-3) D. (-3,-7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com