
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,其中点A的坐标为
与x轴交于A、B两点,其中点A的坐标为![]() ,抛物线的顶点为P.
,抛物线的顶点为P.
![]() 求b的值,并求出点P、B的坐标;
求b的值,并求出点P、B的坐标;
![]() 在x轴下方的抛物线上是否存在点M,使
在x轴下方的抛物线上是否存在点M,使![]() ≌
≌![]() ?如果存在,请直接写出点M的坐标;如果不存在,试说明理由.
?如果存在,请直接写出点M的坐标;如果不存在,试说明理由.

【答案】![]() 存在,
存在,![]()
【解析】
(1)将点A的坐标代入抛物线的解析式可求得b的值,从而得到抛物线的解析式,然后利用配方法对抛物线的解析式进行变形可求得点P的坐标,接下来,令y=0得到关于x的方程可求得点B的横坐标;
(2)过点P作PC⊥x轴,垂足为C,连接AP、BP,作∠PAB的平分线,交PB与点N,交抛物线与点M,连接PM、BM,求得AB、AP、BP的长,然后可证明PN=PB,从而可求得点N的坐标,然后再求得AM的解析式,最后求得直线AM与抛物线的交点M的坐标即可.
![]() 抛物线
抛物线![]() 经过
经过![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 抛物线的表达式为
抛物线的表达式为![]() .
.
![]() ,
,
![]() 点P的坐标为
点P的坐标为![]()
令![]() 得:
得:![]() ,解得
,解得![]() 或
或![]() ,
,
![]() 的坐标为
的坐标为![]() .
.
![]() 存在,点
存在,点![]()
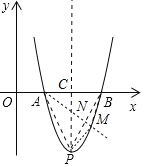
如图:过点P作![]() 轴,垂足为C,连接AP、BP,作
轴,垂足为C,连接AP、BP,作![]() 的平分线,交PB与点N,交抛物线与点M,连接PM、BM.
的平分线,交PB与点N,交抛物线与点M,连接PM、BM.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,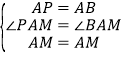 ,
,
![]() ≌
≌![]() .
.
![]() 存在这样的点M,使得
存在这样的点M,使得![]() ≌
≌![]() .
.
![]() ,
,![]() ,点N是PB的中点,
,点N是PB的中点,
![]()
设直线AM的解析式为![]() ,将点A和点N的坐标代入得:
,将点A和点N的坐标代入得:![]() ,解得:
,解得: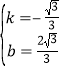 ,
,
![]() 直线AM的解析式为
直线AM的解析式为![]() .
.
将![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() ,解得:
,解得:![]() 或
或![]() 舍去
舍去![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点M的坐标为
点M的坐标为![]()


科目:初中数学 来源: 题型:
【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)在这次调查中,一共调查了 名市民.
(2)扇形统计图中,C组对应的扇形圆心角是 .
(3)请补全条形统计图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划从各班各抽出1名学生作为代表参加学校组织的海外游学计划,明明和华华都是本班的候选人,经过老师与同学们商量,用所学的概率知识设计摸球游戏决定谁去,设计的游戏规则如下:取M、N两个不透明的布袋,分别放入黄色和白色两种除颜色外均相同的乒乓球,其中M布袋中放置3个黄色的乒乓球和2个白色的乒乓球;N布袋中放置1个黄色的乒乓球,3个白色的乒乓球![]() 明明从M布袋摸一个乒乓球,华华从N布袋摸一个乒乓球进行试验,若两人摸出的两个乒乓球都是黄色,则明明去;若两人摸出的两个乒乓球都是白色,则华华去;若两人摸出乒乓球颜色不一样,则放回重复以上动作,直到分出胜负为止
明明从M布袋摸一个乒乓球,华华从N布袋摸一个乒乓球进行试验,若两人摸出的两个乒乓球都是黄色,则明明去;若两人摸出的两个乒乓球都是白色,则华华去;若两人摸出乒乓球颜色不一样,则放回重复以上动作,直到分出胜负为止![]() 根据以上规则回答下列:
根据以上规则回答下列:
![]() 求一次性摸出一个黄色乒乓球和一个白色乒乓球的概率;
求一次性摸出一个黄色乒乓球和一个白色乒乓球的概率;
![]() 判断该游戏是否公平?并说明理由.
判断该游戏是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林局有甲、乙、丙三个植树队,已知甲队植树![]() 棵,乙队植树的棵树比甲队植的棵数的2倍还多8棵,丙队植树的棵数比乙队植的棵数的一半少6棵。
棵,乙队植树的棵树比甲队植的棵数的2倍还多8棵,丙队植树的棵数比乙队植的棵数的一半少6棵。
(1)问甲队植树的棵数多还是丙队植树的棵数多?多多少棵?
(2)三个队一共植树多少棵?
(3)假设三队共植树2546棵,求三个队分别植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年,“即墨古城”在即墨区破土重建,2016年建成,现已成为青岛北部一个重要的旅游景点,为了衡量古城“潮海”门的高度,在数学课外实践活动中,小明分别在如图所示的A,B两点处,利用测角仪对“潮海”,门的最高点C进行了测量,测得![]() ,
,![]() ,若
,若![]() 米,求“潮海”门的最高点C到地面的高度为多少米?
米,求“潮海”门的最高点C到地面的高度为多少米?![]() 结果精确到1米,参考数据:
结果精确到1米,参考数据:![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
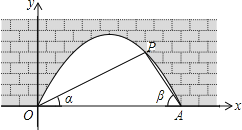
【题目】图中是抛物线拱桥,P处有一照明灯,点P到水面OA的距离为![]() ,从O、A两处观测P处,仰角分别为
,从O、A两处观测P处,仰角分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为
,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为![]() .
.
![]() 求抛物线方程,并求抛物线上的最高点到水面的距离;
求抛物线方程,并求抛物线上的最高点到水面的距离;
![]() 水面上升1m,水面宽多少
水面上升1m,水面宽多少![]() 取
取![]() ,结果精确到
,结果精确到![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…,则第100个点的横坐标为( )

A.12B.13C.14D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com