
【题目】已知抛物线![]() 经过点
经过点![]() 设点
设点![]() ,欲在抛物线的对称轴上确定一点D,使得
,欲在抛物线的对称轴上确定一点D,使得![]() 的值最大,则D点的坐标是______.
的值最大,则D点的坐标是______.
【答案】![]()
【解析】
首先利用待定系数法求得抛物线的解析式,然后可求得抛物线的对称轴方程x=2,又由作点C关于x=2的对称点C′,直线AC′与x=3的交点即为D,求得直线AC′的解析式,即可求得答案.
∵抛物线y=![]() x2+bx经过点A(4,0),
x2+bx经过点A(4,0),
∴![]() ×42+4b=0,
×42+4b=0,
∴b=-2,
∴抛物线的解析式为:y=![]() x2-2x=
x2-2x=![]() (x-2)2-2,
(x-2)2-2,
∴抛物线的对称轴为:直线x=2,
∵点C(1,-4),
∴作点C关于x=2的对称点C′(3,-4),
直线AC′与x=2的交点即为D,
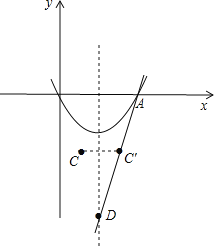
因为任意取一点D(AC与对称轴的交点除外)都可以构成一个△ADC.而在三角形中,两边之差小于第三边,即|AD-CD|<AC′.所以最大值就是在D是AC′延长线上的点的时候取到|AD-C′D|=AC′最大,
设直线AC′的解析式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴直线AC′的解析式为y=4x-16,
当x=2时,y=-8,
∴D点的坐标为(2,-8).
故答案为:(2,-8).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.

(1)分别写出△ABC各个顶点的坐标;
(2)分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标;
(3)求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于D、E.

(1)若AC=12,BC=10,求△EBC的周长;
(2)若∠A=40°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.

(1)请画出平移后的△ABC的图形
(2)写出△A′B′C′各个顶点的坐标;
(3)在x轴上是否存在点P,值![]() ,若存在,请写出P点的坐标,若不存在请说明理由.
,若存在,请写出P点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,其中点A的坐标为
与x轴交于A、B两点,其中点A的坐标为![]() ,抛物线的顶点为P.
,抛物线的顶点为P.
![]() 求b的值,并求出点P、B的坐标;
求b的值,并求出点P、B的坐标;
![]() 在x轴下方的抛物线上是否存在点M,使
在x轴下方的抛物线上是否存在点M,使![]() ≌
≌![]() ?如果存在,请直接写出点M的坐标;如果不存在,试说明理由.
?如果存在,请直接写出点M的坐标;如果不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
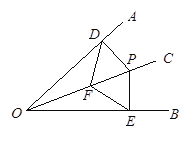
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com