
【题目】已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于D、E.

(1)若AC=12,BC=10,求△EBC的周长;
(2)若∠A=40°,求∠EBC的度数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB =AC,AD⊥BC于点D,AM是△ABC的外角∠CAE的平分线.
(1)求证:AM∥BC;
(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,三角形ABC的顶点坐标分别是A(1,1);B(2,﹣1);C(4,3),将三角形ABC向左平移2个单位长度,再向上平移3个单位长度后得三角形A1B1C1.
(1)画出三角形A1B1C1;
(2)分别写出A1、B1、C1的坐标;
(3)求三角形A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是合同三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1),若运动方向相反,则称它们是镜面合同三角形(如图2),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°.下列各组合同三角形中,是镜面合同三角形的是( )
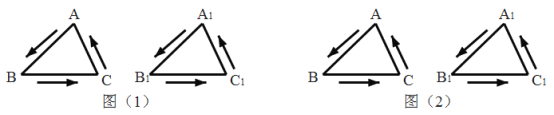
A.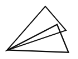 B.
B.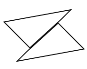 C.
C.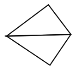 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
(1)证明AE=AF;
(2)若△ABC面积是36cm2,AB=10cm,AC=8cm,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜基地加工厂有工人100人,现对100人进行工作分工,或采摘蔬菜,或对当日采摘的蔬菜进行精加工,每人每天只能做一项工作,若采摘蔬菜,每人每天平均采摘48kg;若对当日采摘的蔬菜进行精加工,每人每天可精加工![]() 每天精加工的蔬菜和没来得及精加工的蔬菜全部售出
每天精加工的蔬菜和没来得及精加工的蔬菜全部售出![]() 已知每千克蔬菜直接出售可获利润1元,精加工后再出售,每千克可获利润3元,设每天安排x名工人进行蔬菜精加工.
已知每千克蔬菜直接出售可获利润1元,精加工后再出售,每千克可获利润3元,设每天安排x名工人进行蔬菜精加工.
![]() 求每天蔬菜精加工后再出售所得利润
求每天蔬菜精加工后再出售所得利润![]() 元
元![]() 与
与![]() 人
人![]() 的函数关系式;
的函数关系式;
![]() 如何安排精加工人数才能使一天所获的利润最大,最大利润是多少?
如何安排精加工人数才能使一天所获的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划从各班各抽出1名学生作为代表参加学校组织的海外游学计划,明明和华华都是本班的候选人,经过老师与同学们商量,用所学的概率知识设计摸球游戏决定谁去,设计的游戏规则如下:取M、N两个不透明的布袋,分别放入黄色和白色两种除颜色外均相同的乒乓球,其中M布袋中放置3个黄色的乒乓球和2个白色的乒乓球;N布袋中放置1个黄色的乒乓球,3个白色的乒乓球![]() 明明从M布袋摸一个乒乓球,华华从N布袋摸一个乒乓球进行试验,若两人摸出的两个乒乓球都是黄色,则明明去;若两人摸出的两个乒乓球都是白色,则华华去;若两人摸出乒乓球颜色不一样,则放回重复以上动作,直到分出胜负为止
明明从M布袋摸一个乒乓球,华华从N布袋摸一个乒乓球进行试验,若两人摸出的两个乒乓球都是黄色,则明明去;若两人摸出的两个乒乓球都是白色,则华华去;若两人摸出乒乓球颜色不一样,则放回重复以上动作,直到分出胜负为止![]() 根据以上规则回答下列:
根据以上规则回答下列:
![]() 求一次性摸出一个黄色乒乓球和一个白色乒乓球的概率;
求一次性摸出一个黄色乒乓球和一个白色乒乓球的概率;
![]() 判断该游戏是否公平?并说明理由.
判断该游戏是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB两端点坐标分别为A(﹣1,5)、B(3,3),线段CD两端点坐标分别为C(5,3)、D (3,﹣1)数学课外兴趣小组研究这两线段发现:其中一条线段绕着某点旋转一个角度可得到另一条线段,请写出旋转中心的坐标________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com