
【题目】某蔬菜基地加工厂有工人100人,现对100人进行工作分工,或采摘蔬菜,或对当日采摘的蔬菜进行精加工,每人每天只能做一项工作,若采摘蔬菜,每人每天平均采摘48kg;若对当日采摘的蔬菜进行精加工,每人每天可精加工![]() 每天精加工的蔬菜和没来得及精加工的蔬菜全部售出
每天精加工的蔬菜和没来得及精加工的蔬菜全部售出![]() 已知每千克蔬菜直接出售可获利润1元,精加工后再出售,每千克可获利润3元,设每天安排x名工人进行蔬菜精加工.
已知每千克蔬菜直接出售可获利润1元,精加工后再出售,每千克可获利润3元,设每天安排x名工人进行蔬菜精加工.
![]() 求每天蔬菜精加工后再出售所得利润
求每天蔬菜精加工后再出售所得利润![]() 元
元![]() 与
与![]() 人
人![]() 的函数关系式;
的函数关系式;
![]() 如何安排精加工人数才能使一天所获的利润最大,最大利润是多少?
如何安排精加工人数才能使一天所获的利润最大,最大利润是多少?
【答案】![]() ;
;![]() 安排60人进行精加工,40人采摘蔬菜,一天所获利润最大,最大利润5760元.
安排60人进行精加工,40人采摘蔬菜,一天所获利润最大,最大利润5760元.
【解析】
(1)因为对采摘后的蔬菜进行精加工,每人每天可精加工32kg,精加工后再出售,每千克可获利润3元,所以每天蔬菜精加工后再出售所得利润y(元)与x(人)的函数关系式是y=3×32x,整理即可;
(2)因为采摘蔬菜,每人每天平均采摘48kg,每千克蔬菜直接出售可获利润1元,所以w=96x+[48(100-x)-32x]×1,整理即可得要求的解析式,然后利用该函数中y随x的变化规律及自变量的取值范围即可解决问题.
![]() ,
,
![]() ;
;
![]() 设每天全部售出后获利w元,则
设每天全部售出后获利w元,则![]() ,
,
由题意知:![]() ,
,
解得![]() ,
,
![]() ,
,![]() ,
,
![]() 随x的增大而增大,
随x的增大而增大,
![]() 当
当![]() 时,w有最大值,
时,w有最大值,![]() 元
元![]() .
.
![]() 安排60人进行精加工,40人采摘蔬菜,一天所获利润最大,最大利润5760元.
安排60人进行精加工,40人采摘蔬菜,一天所获利润最大,最大利润5760元.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】甲乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的22张卡片,其中写有“锤子”石头”、“剪子”、“布”的卡片张数分别为4、5、6、7.两人先后各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:
“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“剪子”的概率是多少?
(2)若甲先摸出了“剪子”,则乙获胜的概率是多少?
(3)若甲先摸,则他摸出哪种卡片获胜的可能性最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC.
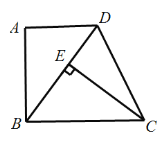
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于D、E.

(1)若AC=12,BC=10,求△EBC的周长;
(2)若∠A=40°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地路程y(千米)与行驶时间x(小时)的函数关系图象.
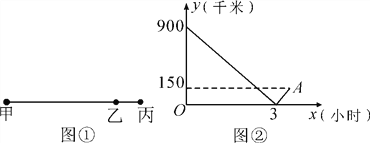
(1)填空:甲、丙两地距离_______千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)在图中画出△ABC与关于y轴对称的图形△A1B1C1,并写出顶点A1、B1、C1的坐标;
(2)若将线段A1C1平移后得到线段A2C2,且A2(a,2),C2(-2,b),求a+b的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com