
【题目】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
(1)证明AE=AF;
(2)若△ABC面积是36cm2,AB=10cm,AC=8cm,求DE的长.

【答案】(1)见解析;(2)4
【解析】
本题主要考察角平分线的性质定理和三角形面积的求法,可以根据角平分线的性质定理结合全等进行证明.
(1)证明:∵在△ABC中,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°,AD=AD
∴△ADE![]() △ADF,
△ADF,
∴AE=AF;
(2)解:∵在△ABC中,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵△ABC面积是36cm2,AB=10cm,AC=8cm,
∴S△ABC=S△ADB+S△ACD=![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() DE(AB+AC)=
DE(AB+AC)=![]() ×DE×(10+8)=9DE=36,
×DE×(10+8)=9DE=36,
∴DE=4(cm).


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中:①m2是有理数;②m的值满足m2﹣12=0;③m满足不等式组![]() ;④m是12的算术平方根. 正确有几个( )
;④m是12的算术平方根. 正确有几个( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.

(1)乙步行的速度为_ __米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC.
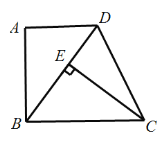
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于D、E.

(1)若AC=12,BC=10,求△EBC的周长;
(2)若∠A=40°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
情形展示:
情形一:如图![]() ,在
,在![]() 中,沿等腰三角形ABC的顶角
中,沿等腰三角形ABC的顶角![]() 的平分线
的平分线![]() 折叠,若点B与点C重合,则称
折叠,若点B与点C重合,则称![]() 是
是![]() 的“好角”,如图
的“好角”,如图![]() ,在
,在![]() 中,先沿
中,先沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分,再将余下部分沿
折叠,剪掉重复部分,再将余下部分沿![]() 的平分线
的平分线![]() 折叠,若点
折叠,若点![]() 与点C重合,则称
与点C重合,则称![]() 是
是![]() 的“好角”.
的“好角”.
情形二:如图![]() ,在
,在![]() 中,先沿
中,先沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分,再将余下部分沿
折叠,剪掉重复部分,再将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分
折叠,剪掉重复部分![]() 重复折叠n次,最终若点
重复折叠n次,最终若点![]() 与点C重合,则称
与点C重合,则称![]() 是
是![]() 的“好角”,探究发现:
的“好角”,探究发现:![]() 不妨设
不妨设![]()
![]() 如图
如图![]() ,若
,若![]() 是
是![]() 的“好角”,则
的“好角”,则![]() 与
与![]() 的数量关系是:______.
的数量关系是:______.
![]() 如图
如图![]() ,若
,若![]() 是
是![]() 的“好角”,则
的“好角”,则![]() 与
与![]() 的数量关系是:______.
的数量关系是:______.
![]() 如图
如图![]() ,若
,若![]() 是
是![]() 的“好角”,则
的“好角”,则![]() 与
与![]() 的数量关系是:______.
的数量关系是:______.
应用提升:
![]() 如果一个三角形的三个角分别为
如果一个三角形的三个角分别为![]() ,
,![]() ,
,![]() ,我们发现
,我们发现![]() 和
和![]() 的两个角都是此三角形的“好角”;如果有一个三角形,它的三个角均是此三角形的“好角”,且已知最小的角是
的两个角都是此三角形的“好角”;如果有一个三角形,它的三个角均是此三角形的“好角”,且已知最小的角是![]() ,求另外两个角的度数.
,求另外两个角的度数.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com