
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
ЧщаЮеЙЪОЃК
ЧщаЮвЛЃКШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌбиЕШбќШ§НЧаЮABCЕФЖЅНЧ
жаЃЌбиЕШбќШ§НЧаЮABCЕФЖЅНЧ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() елЕўЃЌШєЕуBгыЕуCжиКЯЃЌдђГЦ
елЕўЃЌШєЕуBгыЕуCжиКЯЃЌдђГЦ![]() ЪЧ
ЪЧ![]() ЕФЁАКУНЧЁБЃЌШчЭМ
ЕФЁАКУНЧЁБЃЌШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌЯШби
жаЃЌЯШби![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() елЕўЃЌМєЕєжиИДВПЗжЃЌдйНЋгрЯТВПЗжби
елЕўЃЌМєЕєжиИДВПЗжЃЌдйНЋгрЯТВПЗжби![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() елЕўЃЌШєЕу
елЕўЃЌШєЕу![]() гыЕуCжиКЯЃЌдђГЦ
гыЕуCжиКЯЃЌдђГЦ![]() ЪЧ
ЪЧ![]() ЕФЁАКУНЧЁБЃЎ
ЕФЁАКУНЧЁБЃЎ
ЧщаЮЖўЃКШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌЯШби
жаЃЌЯШби![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() елЕўЃЌМєЕєжиИДВПЗжЃЌдйНЋгрЯТВПЗжби
елЕўЃЌМєЕєжиИДВПЗжЃЌдйНЋгрЯТВПЗжби![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() елЕўЃЌМєЕєжиИДВПЗж
елЕўЃЌМєЕєжиИДВПЗж![]() жиИДелЕўnДЮЃЌзюжеШєЕу
жиИДелЕўnДЮЃЌзюжеШєЕу![]() гыЕуCжиКЯЃЌдђГЦ
гыЕуCжиКЯЃЌдђГЦ![]() ЪЧ
ЪЧ![]() ЕФЁАКУНЧЁБЃЌЬНОПЗЂЯжЃК
ЕФЁАКУНЧЁБЃЌЬНОПЗЂЯжЃК![]() ВЛЗСЩш
ВЛЗСЩш![]()
![]() ШчЭМ
ШчЭМ![]() ЃЌШє
ЃЌШє![]() ЪЧ
ЪЧ![]() ЕФЁАКУНЧЁБЃЌдђ
ЕФЁАКУНЧЁБЃЌдђ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧЃК______ЃЎ
ЕФЪ§СПЙиЯЕЪЧЃК______ЃЎ
![]() ШчЭМ
ШчЭМ![]() ЃЌШє
ЃЌШє![]() ЪЧ
ЪЧ![]() ЕФЁАКУНЧЁБЃЌдђ
ЕФЁАКУНЧЁБЃЌдђ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧЃК______ЃЎ
ЕФЪ§СПЙиЯЕЪЧЃК______ЃЎ
![]() ШчЭМ
ШчЭМ![]() ЃЌШє
ЃЌШє![]() ЪЧ
ЪЧ![]() ЕФЁАКУНЧЁБЃЌдђ
ЕФЁАКУНЧЁБЃЌдђ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧЃК______ЃЎ
ЕФЪ§СПЙиЯЕЪЧЃК______ЃЎ
гІгУЬсЩ§ЃК
![]() ШчЙћвЛИіШ§НЧаЮЕФШ§ИіНЧЗжБ№ЮЊ
ШчЙћвЛИіШ§НЧаЮЕФШ§ИіНЧЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЮвУЧЗЂЯж
ЃЌЮвУЧЗЂЯж![]() КЭ
КЭ![]() ЕФСНИіНЧЖМЪЧДЫШ§НЧаЮЕФЁАКУНЧЁБЃЛШчЙћгавЛИіШ§НЧаЮЃЌЫќЕФШ§ИіНЧОљЪЧДЫШ§НЧаЮЕФЁАКУНЧЁБЃЌЧввбжЊзюаЁЕФНЧЪЧ
ЕФСНИіНЧЖМЪЧДЫШ§НЧаЮЕФЁАКУНЧЁБЃЛШчЙћгавЛИіШ§НЧаЮЃЌЫќЕФШ§ИіНЧОљЪЧДЫШ§НЧаЮЕФЁАКУНЧЁБЃЌЧввбжЊзюаЁЕФНЧЪЧ![]() ЃЌЧѓСэЭтСНИіНЧЕФЖШЪ§ЃЎ
ЃЌЧѓСэЭтСНИіНЧЕФЖШЪ§ЃЎ



ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ ЃЈ2ЃЉ
ЃЛ ЃЈ2ЃЉ![]() ЃЛ ЃЈ3ЃЉ
ЃЛ ЃЈ3ЃЉ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉИУШ§НЧаЮЕФСэЭтСНИіНЧЕФЖШЪ§ЗжБ№ЮЊЃК![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩИљОнЬтвтПЩжЊЃЌ![]() гы
гы![]() жиКЯЃЌМД
жиКЯЃЌМД![]() ЃЛ
ЃЛ
ЃЈ2ЃЉИљОнЬтвтЕУ![]() ЃЌ
ЃЌ![]() ЃЌвђЮЊ
ЃЌвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЛ
ЃЛ
ЃЈ3ЃЉИљОнЩЯУцНсТлПЩжЊЃКЕБ![]() ЪЧЁАКУНЧЁБЃЌелЕўЕФДЮЪ§ОЭЪЧЁЯBЮЊЁЯCЕФБЖЪ§ЃЌМД
ЪЧЁАКУНЧЁБЃЌелЕўЕФДЮЪ§ОЭЪЧЁЯBЮЊЁЯCЕФБЖЪ§ЃЌМД![]() ЃЛ
ЃЛ
ЃЈ4ЃЉгЩЬтвтПЩжЊЃЌШ§НЧаЮЕФСэЭтСНИіНЧЖМЪЧ12ЁуБЖЪ§ЃЌдђПЩЩшСэСННЧЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌИљОнШ§НЧаЮЕФФкНЧКЭЖЈРэЗжЧщПіЧѓГіmЃЌnЕФжЕМДПЩ.
ЃЌИљОнШ§НЧаЮЕФФкНЧКЭЖЈРэЗжЧщПіЧѓГіmЃЌnЕФжЕМДПЩ.
![]() ШчЭМ1жаЃЌ
ШчЭМ1жаЃЌ![]() ЪЧ
ЪЧ![]() ЕФЁАКУНЧЁБЃЌ
ЕФЁАКУНЧЁБЃЌ
![]() гы
гы![]() жиКЯЃЌ
жиКЯЃЌ
![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊ![]() ЃЛ
ЃЛ
![]() ШчЭМ2жаЃЌ
ШчЭМ2жаЃЌ![]() би
би![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() елЕўЃЌ
елЕўЃЌ
![]() ЃЌ
ЃЌ
гж![]() НЋгрЯТВПЗжби
НЋгрЯТВПЗжби![]() ЕФЦНЗжЯпA1B2елЕўЃЌДЫЪБЕу
ЕФЦНЗжЯпA1B2елЕўЃЌДЫЪБЕу![]() гыЕуCжиКЯЃЌ
гыЕуCжиКЯЃЌ
![]() ЃЛ
ЃЛ
![]() ЭтНЧЖЈРэ
ЭтНЧЖЈРэ![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
![]() ИљОнЩЯУцНсТлПЩжЊЃК
ИљОнЩЯУцНсТлПЩжЊЃК
ЕБ1ДЮелЕўЪБЃЌ![]() ЪЧЁАКУНЧЁБЃЌдђга
ЪЧЁАКУНЧЁБЃЌдђга![]() ЃЌ
ЃЌ
ЕБ2ДЮелЕўЪБЃЌ![]() ЪЧЁАКУНЧЁБЃЌдђга
ЪЧЁАКУНЧЁБЃЌдђга![]() ЃЌ
ЃЌ
ЕБ3ДЮелЕўЪБЃЌ![]() ЪЧЁАКУНЧЁБЃЌдђга
ЪЧЁАКУНЧЁБЃЌдђга![]() ЃЌ
ЃЌ
![]()
ЕБnДЮелЕўЪБЃЌ![]() ЪЧЁАКУНЧЁБЃЌдђга
ЪЧЁАКУНЧЁБЃЌдђга![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊ![]() ЃЎ
ЃЎ
![]() вђЮЊзюаЁНЧЪЧ
вђЮЊзюаЁНЧЪЧ![]() ЪЧ
ЪЧ![]() ЕФКУНЧЃЌ
ЕФКУНЧЃЌ
ИљОнКУНЧЖЈвхЃЌдђПЩЩшСэСННЧЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЦфжаmЁЂnЖМЪЧе§ећЪ§
ЦфжаmЁЂnЖМЪЧе§ећЪ§![]() ЃЌ
ЃЌ
гЩЬтвтЃЌЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпmЁЂnЖМЪЧе§ећЪ§ЃЌЫљвдmгы![]() ЪЧ14ЕФећЪ§вђзгЃЌ
ЪЧ14ЕФећЪ§вђзгЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌЛђ
ЃЌЛђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ![]() ЃЌЛђ
ЃЌЛђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌЛђ
ЃЌЛђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђИУШ§НЧаЮЕФСэЭтСНИіНЧЕФЖШЪ§ЗжБ№ЮЊЃК![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() .
.


 гХЩњРждАЯЕСаД№АИ
гХЩњРждАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЮЊЁЯBACЕФЦНЗжЯпЃЌDEЁЭABгкEЃЌDFЁЭACгкFЃЌ
ЃЈ1ЃЉжЄУїAE=AFЃЛ
ЃЈ2ЃЉШєЁїABCУцЛ§ЪЧ36cm2ЃЌAB=10cmЃЌAC=8cmЃЌЧѓDEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЬНОП
![]() ЧыдкЭМ
ЧыдкЭМ![]() ЕФе§ЗНаЮABCDЕФЖдНЧЯпBDЩЯзївЛЕуPЃЌЪЙ
ЕФе§ЗНаЮABCDЕФЖдНЧЯпBDЩЯзївЛЕуPЃЌЪЙ![]() зюаЁЃЛ
зюаЁЃЛ
![]() ШчЭМ
ШчЭМ![]() ЃЌЕуPЮЊОиаЮABCDЕФЖдНЧЯпBDЩЯвЛЖЏЕуЃЌ
ЃЌЕуPЮЊОиаЮABCDЕФЖдНЧЯпBDЩЯвЛЖЏЕуЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕуEЮЊBCБпЕФжаЕуЃЌЧызївЛЕуPЃЌЪЙ
ЃЌЕуEЮЊBCБпЕФжаЕуЃЌЧызївЛЕуPЃЌЪЙ![]() зюаЁЃЌВЂЧѓетИізюаЁжЕЃЛ
зюаЁЃЌВЂЧѓетИізюаЁжЕЃЛ
ЮЪЬтНтОі
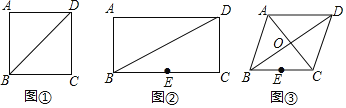
![]() ШчЭМ
ШчЭМ![]() ЃЌРюЪІИЕгавЛПщБпГЄЮЊ1000УзЕФСтаЮВЩеЊдАABCDЃЌ
ЃЌРюЪІИЕгавЛПщБпГЄЮЊ1000УзЕФСтаЮВЩеЊдАABCDЃЌ![]() УзЃЌBDЮЊаЁТЗЃЌBCЕФжаЕуEЮЊвЛЫЎГиЃЌРюЪІИЕЯждкзМБИдкаЁТЗBDЩЯНЈвЛИігЮПЭСйЪБанЯЂФЩСЙЪвPЃЌЮЊСЫНкЪЁЭСЕиЃЌЪЙанЯЂФЩСЙЪвPЕНЫЎГиEгыДѓУХCЕФОрРыжЎКЭзюЖЬЃЌФЧУДЪЧЗёДцдкЗћКЯЬѕМўЕФЕуPЃПШєДцдкЃЌЧызїГіЕуPЕФЮЛжУЃЌВЂЧѓГіетИізюЖЬОрРыЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
УзЃЌBDЮЊаЁТЗЃЌBCЕФжаЕуEЮЊвЛЫЎГиЃЌРюЪІИЕЯждкзМБИдкаЁТЗBDЩЯНЈвЛИігЮПЭСйЪБанЯЂФЩСЙЪвPЃЌЮЊСЫНкЪЁЭСЕиЃЌЪЙанЯЂФЩСЙЪвPЕНЫЎГиEгыДѓУХCЕФОрРыжЎКЭзюЖЬЃЌФЧУДЪЧЗёДцдкЗћКЯЬѕМўЕФЕуPЃПШєДцдкЃЌЧызїГіЕуPЕФЮЛжУЃЌВЂЧѓГіетИізюЖЬОрРыЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌABЕФДЙжБЦНЗжЯпНЛABгкNЃЌНЛACгкMЃЎ
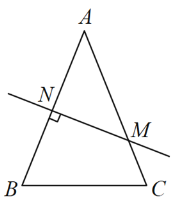
ЃЈ1ЃЉШєЁЯC ЃН70ЁуЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЁЯC ЃНІСЃЌЧыгУКЌІСЕФЪНзгБэЪО![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСЌНгMBЃЌШєAB ЃН8ЃЌBC ЃН6ЃЎ
ЂйЧѓЁї![]() ЕФжмГЄЃЛ
ЕФжмГЄЃЛ
ЂкдкжБЯп![]() ЩЯЪЧЗёДцдкЕуPЃЌЪЙЃЈPB+CPЃЉЕФжЕзюаЁЃПШєДцдкЃЌБъГіЕуPЕФЮЛжУВЂЧѓЃЈPB+CPЃЉЕФзюаЁжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЩЯЪЧЗёДцдкЕуPЃЌЪЙЃЈPB+CPЃЉЕФжЕзюаЁЃПШєДцдкЃЌБъГіЕуPЕФЮЛжУВЂЧѓЃЈPB+CPЃЉЕФзюаЁжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉЃЈЉ![]() ЃЉЃЈЉ
ЃЉЃЈЉ![]() ЃЉ+|
ЃЉ+|![]() Љ1|+ЃЈ3ЉІаЃЉ0ЃЎ
Љ1|+ЃЈ3ЉІаЃЉ0ЃЎ
ЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉЃЈ2![]() +3ЃЉ2019ЃЈ2
+3ЃЉ2019ЃЈ2![]() Љ3ЃЉ2020ЉЃЈ3
Љ3ЃЉ2020ЉЃЈ3![]() Љ2ЃЉ2ЃЎ
Љ2ЃЉ2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЯпЖЮABСНЖЫЕузјБъЗжБ№ЮЊAЃЈЉ1ЃЌ5ЃЉЁЂBЃЈ3ЃЌ3ЃЉЃЌЯпЖЮCDСНЖЫЕузјБъЗжБ№ЮЊCЃЈ5ЃЌ3ЃЉЁЂD ЃЈ3ЃЌЉ1ЃЉЪ§бЇПЮЭтаЫШЄаЁзщбаОПетСНЯпЖЮЗЂЯжЃКЦфжавЛЬѕЯпЖЮШЦзХФГЕуа§зЊвЛИіНЧЖШПЩЕУЕНСэвЛЬѕЯпЖЮЃЌЧыаДГіа§зЊжааФЕФзјБъ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌAEЦНЗжЁЯBADЃЌDEЦНЗжЁЯADC.

ЃЈ1ЃЉШчЙћЁЯBЃЋЁЯCЃН120ЁуЃЌдђЁЯAEDЕФЖШЪ§ЃН______.ЃЈжБНгаДГіНсЙћЃЉ
ЃЈ2ЃЉИљОнЂХЕФНсТлЃЌВТЯыЁЯBЃЋЁЯCгыЁЯAEDжЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЮЊжБНЧШ§НЧаЮЃЌЁЯC=90ЁуЃЌBC=2cmЃЌЁЯA=30ЁуЃЌЫФБпаЮDEFGЮЊОиаЮЃЌDE=2![]() cmЃЌEF=6cmЃЌЧвЕуCЁЂBЁЂEЁЂFдкЭЌвЛЬѕжБЯпЩЯЃЌЕуBгыЕуEжиКЯЃЎRtЁїABCвдУПУы1cmЕФЫйЖШбиОиаЮDEFGЕФБпEFЯђгвЦНвЦЃЌЕБЕуCгыЕуFжиКЯЪБЭЃжЙЃЎЩшRtЁїABCгыОиаЮDEFGЕФжиЕўВПЗжЕФУцЛ§ЮЊycm2ЃЌдЫЖЏЪБМфxsЃЎФмЗДгГycm2гыxsжЎМфКЏЪ§ЙиЯЕЕФДѓжТЭМЯѓЪЧЃЈЁЁЁЁЃЉ
cmЃЌEF=6cmЃЌЧвЕуCЁЂBЁЂEЁЂFдкЭЌвЛЬѕжБЯпЩЯЃЌЕуBгыЕуEжиКЯЃЎRtЁїABCвдУПУы1cmЕФЫйЖШбиОиаЮDEFGЕФБпEFЯђгвЦНвЦЃЌЕБЕуCгыЕуFжиКЯЪБЭЃжЙЃЎЩшRtЁїABCгыОиаЮDEFGЕФжиЕўВПЗжЕФУцЛ§ЮЊycm2ЃЌдЫЖЏЪБМфxsЃЎФмЗДгГycm2гыxsжЎМфКЏЪ§ЙиЯЕЕФДѓжТЭМЯѓЪЧЃЈЁЁЁЁЃЉ

A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
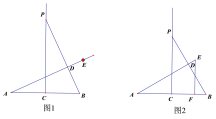
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕуЃЌЙ§Еу
ЕФжаЕуЃЌЙ§Еу![]() зї
зї![]() ЕФДЙЯп
ЕФДЙЯп![]() ЃЌдкЩфЯп
ЃЌдкЩфЯп![]() ЩЯгавЛИіЖЏЕу
ЩЯгавЛИіЖЏЕу![]() (Еу
(Еу![]() ВЛгыЖЫЕу
ВЛгыЖЫЕу![]() жиКЯ)ЃЌСЌНг
жиКЯ)ЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЕФДЙЯпЃЌДЙзуЮЊЕу
ЕФДЙЯпЃЌДЙзуЮЊЕу![]() ЃЌдкЩфЯп
ЃЌдкЩфЯп![]() ЩЯШЁЕу
ЩЯШЁЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌвбжЊ
ЃЌвбжЊ![]()
(1)ЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
(2)Й§Еу![]() зї
зї![]() ДЙжБгкжБЯп
ДЙжБгкжБЯп![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌдкЕу
ЃЌдкЕу![]() ЕФдЫЖЏЙ§ГЬжаЃЌ
ЕФдЫЖЏЙ§ГЬжаЃЌ![]() ЕФДѓаЁЫцЕу
ЕФДѓаЁЫцЕу![]() ЕФдЫЖЏЖјБфЛЏЃЌдкетИіБфЛЏЙ§ГЬжаЯпЖЮ
ЕФдЫЖЏЖјБфЛЏЃЌдкетИіБфЛЏЙ§ГЬжаЯпЖЮ![]() ЕФГЄЖШЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓГі
ЕФГЄЖШЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓГі![]() ЕФГЄЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛ
ЕФГЄЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛ
(3)ШчЭМ2ЃЌЕБ![]() ЪБЃЌЩшжБЯп
ЪБЃЌЩшжБЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§.
ЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com