
����Ŀ������̽��
![]() ����ͼ
����ͼ![]() ��������ABCD�ĶԽ���BD����һ��P��ʹ
��������ABCD�ĶԽ���BD����һ��P��ʹ![]() ��С��
����
![]() ��ͼ
��ͼ![]() ����PΪ����ABCD�ĶԽ���BD��һ���㣬
����PΪ����ABCD�ĶԽ���BD��һ���㣬![]() ��
��![]() ����EΪBC�ߵ��е㣬����һ��P��ʹ
����EΪBC�ߵ��е㣬����һ��P��ʹ![]() ��С�����������Сֵ��
��С�����������Сֵ��
������
![]() ��ͼ
��ͼ![]() ����ʦ����һ��߳�Ϊ1000�����β�ժABCD��
����ʦ����һ��߳�Ϊ1000�����β�ժABCD��![]() �ף�BDΪС·��BC���е�EΪһˮ�أ���ʦ����������С·BD�Ͻ�һ���ο���ʱ��Ϣ������P��Ϊ�˽�ʡ���أ�ʹ��Ϣ������P��ˮ��E�����C�ľ���֮����̣���ô�Ƿ���ڷ��������ĵ�P�������ڣ���������P��λ�ã�����������̾��룻�������ڣ���˵�����ɣ�
�ף�BDΪС·��BC���е�EΪһˮ�أ���ʦ����������С·BD�Ͻ�һ���ο���ʱ��Ϣ������P��Ϊ�˽�ʡ���أ�ʹ��Ϣ������P��ˮ��E�����C�ľ���֮����̣���ô�Ƿ���ڷ��������ĵ�P�������ڣ���������P��λ�ã�����������̾��룻�������ڣ���˵�����ɣ�
���𰸡��⣺![]() ������
������![]()
![]() ����СֵΪ3��
����СֵΪ3��![]() ���ڣ�����̾���ԼΪ985��
���ڣ�����̾���ԼΪ985��
��������
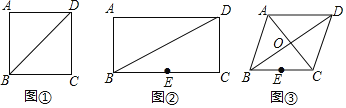
��1����������֮���߶���̣����ɵó����ۣ�
��2����ȷ������P��λ�ã��������CBD=30�㣬�����жϳ���BCC'�ǵȱ������Σ����ɵó����ۣ�
��3����ȷ������P��λ�ã������OA��OB����������������AH������ù��ɶ������ɵó����ۣ�
�⣺![]() ��ͼ
��ͼ![]() ������AC��BD�ڵ�P�����P������Ҫ�����ĵ㣬
������AC��BD�ڵ�P�����P������Ҫ�����ĵ㣬
���ɣ���BD����ȡһ�����ڵ�P�ĵ�Q������AQ��CQ��
![]() ��
��
![]() ��ͼ
��ͼ![]()
 ��
��
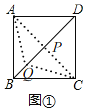
����C����BD�ĶԳƵ�C'������EC'��BD�ڵ�P������C'P��
�ߵ�C���C'����BD�ĶԳƵ㣬
��CP=C'P��
��C'P+PE=C'P'+P'E=C'E��
��BD����ȡ���ڵ�P��P'������P'E��P'C��C'P'��
��C'P'+P'E=P'C+P'E��C'E��
���P������Ҫ�����ĵ㣬EC'�ij���PE+PC����Сֵ��
���ı���ABCD�Ǿ��Σ�![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
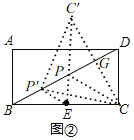
�ߵ�C�͵�C'����BD�Գƣ�
��CC'��BD��G��
��BD��CC'�Ĵ�ֱƽ���ߣ�����BC'��
���C'BD=��CBD=30�㣬BC'=BC��
���C'BC=60�㣬
���BCC'�ǵȱ������Σ�
�ߵ�E��BC���е㣬
��CE��BC��
![]() ��
��
![]() ��
��
����![]() ����СֵΪ3��
����СֵΪ3��
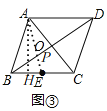
![]() ���ڣ���ͼ
���ڣ���ͼ![]() ������AE��BD��P����P������Ҫ�����ĵ㣬AE�ij��Ⱦ�����Ϣ������P��ˮ��E�����C�ľ���֮����̵�ֵ��
������AE��BD��P����P������Ҫ�����ĵ㣬AE�ij��Ⱦ�����Ϣ������P��ˮ��E�����C�ľ���֮����̵�ֵ��
 ��
��
![]() �ı���ABCD�����Σ�
�ı���ABCD�����Σ�
![]() ��C����BD�ĶԳƵ�ΪA������AE����BD��P����P������Ҫ�����ĵ㣬
��C����BD�ĶԳƵ�ΪA������AE����BD��P����P������Ҫ�����ĵ㣬
![]() �ף�
�ף�![]() �ף�
�ף�![]() ��Q��
��Q��
![]() �ף�
�ף�![]() �ף�
�ף�
����A��![]() ��H��
��H��
![]() ��
��
![]() �ף�
�ף�
��![]() �У����ݹ��ɶ����ã�
�У����ݹ��ɶ����ã�![]() �ף�
�ף�
![]() �ף�
�ף�
��![]() ��
�У�![]() �ף�
�ף�
�������ڵ�P������̾���ԼΪ985�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������������A��B��C��ͬһ��·�����ס��������οʹӾ���A�������ײ��е�����C;�ҳ˾����۹�ȵ�����B����B��ͣ��һ��ʱ������ٲ��е�����C���ס�������ͬʱ���ᄚ��C���ס������˾ྰ��A��·��y(��)��׳�����ʱ��x(��)֮��ĺ���ͼ����ͼ��ʾ��

��1���Ҳ��е��ٶ�Ϊ_ __��/����
��2�����ҳ˾����۹ʱy��x֮��ĺ�����ϵʽ��
��3���׳����ʱ�����ҵ�һ������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�![]() ��ƽ���߽�AD�ڵ�E����BA���ӳ����ڵ�F��
��ƽ���߽�AD�ڵ�E����BA���ӳ����ڵ�F��![]() ��
��![]() ����AF�ij�����
����AF�ij�����![]() ����
����![]()

A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪AE��AB��AF��AC��AE=AB��AF=AC.��֤����1��EC=BF����2��EC��BF.
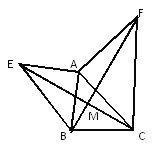
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ǹ��Ϊ8��8�������������������������а�����Ҫ�������
(1)�������н���ƽ��ֱ������ϵ��ʹA������Ϊ(��2��4)��B������Ϊ(��4��2)��
(2)�ڵڶ������ڵĸ���ϻ�һ��C��ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ�������������������C���������� ����
(3)���ABC��BC���ϵĸ߳���
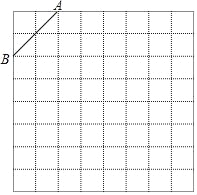
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ij�˿ͳ˸����г��Ӽؾ����ҵص����أ��г�������ʻ��ͼ��Ϊ�г����ҵ�·��y(ǧ��)����ʻʱ��x(Сʱ)�ĺ�����ϵͼ��
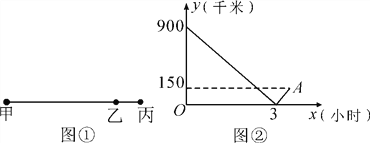
(1)��գ��ס������ؾ���_______ǧ�ף�
(2)������г����ҵص�·��y����ʻʱ��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BC=EC����BCE=��ACD�����ֻ����һ��������ʹ��ABC �� ��DEC�������ӵ���������Ϊ�� ��
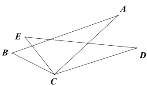
A. ��B=��E B. AC=DC C. ��A=��D D. AB=DE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
����չʾ��
����һ����ͼ![]() ����
����![]() �У��ص���������ABC�Ķ���
�У��ص���������ABC�Ķ���![]() ��ƽ����
��ƽ����![]() �۵�������B���C�غϣ����
�۵�������B���C�غϣ����![]() ��
��![]() �ġ��ýǡ�����ͼ
�ġ��ýǡ�����ͼ![]() ����
����![]() ������
�У�����![]() ��ƽ����
��ƽ����![]() �۵��������ظ����֣��ٽ����²�����
�۵��������ظ����֣��ٽ����²�����![]() ��ƽ����
��ƽ����![]() �۵�������
�۵�������![]() ���C�غϣ����
���C�غϣ����![]() ��
��![]() �ġ��ýǡ���
�ġ��ýǡ���
���ζ�����ͼ![]() ����
����![]() ������
�У�����![]() ��ƽ����
��ƽ����![]() �۵��������ظ����֣��ٽ����²�����
�۵��������ظ����֣��ٽ����²�����![]() ��ƽ����
��ƽ����![]() �۵��������ظ�����
�۵��������ظ�����![]() �ظ��۵�n�Σ���������
�ظ��۵�n�Σ���������![]() ���C�غϣ����
���C�غϣ����![]() ��
��![]() �ġ��ýǡ���̽�����֣�
�ġ��ýǡ���̽�����֣�![]() ������
������![]()
![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() �ġ��ýǡ�����
�ġ��ýǡ�����![]() ��
��![]() ��������ϵ�ǣ�______��
��������ϵ�ǣ�______��
![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() �ġ��ýǡ�����
�ġ��ýǡ�����![]() ��
��![]() ��������ϵ�ǣ�______��
��������ϵ�ǣ�______��
![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() �ġ��ýǡ�����
�ġ��ýǡ�����![]() ��
��![]() ��������ϵ�ǣ�______��
��������ϵ�ǣ�______��
Ӧ��������
![]() ���һ�������ε������Ƿֱ�Ϊ
���һ�������ε������Ƿֱ�Ϊ![]() ��
��![]() ��
��![]() �����Ƿ���
�����Ƿ���![]() ��
��![]() �������Ƕ��Ǵ������εġ��ýǡ��������һ�������Σ����������Ǿ��Ǵ������εġ��ýǡ�������֪��С�Ľ���
�������Ƕ��Ǵ������εġ��ýǡ��������һ�������Σ����������Ǿ��Ǵ������εġ��ýǡ�������֪��С�Ľ���![]() �������������ǵĶ�����
�������������ǵĶ�����



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A=��B��AE=BE����D��AC���ϣ���1=��2��AE��BD�ཻ�ڵ�O��
��1����֤����AEC�ա�BED��
��2������1=42�㣬���BDE�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com