
【题目】某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.

(1)乙步行的速度为_ __米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙第一次相遇?
【答案】(1)80;(2)y=30x-6000;(3)甲出发25分钟与乙第一次相遇.
【解析】试题分析:(1)根据速度=路程÷时间,即可求出乙步行的速度;
(2)观察函数图象,找出两点的坐标,利用待定系数即可求出乙乘景区观光车时y与x之间的函数关系式;
(3)根据速度=路程÷时间求出甲步行的速度,进而找出甲步行时y与x之间的函数关系式,联立两函数关系式成方程组,通过解方程组即可求出二者第一次相遇的时间.
试题解析:解:(1)乙步行的速度为:(5400﹣3000)÷(90﹣60)=80(米/分).
故答案为:80.
(2)设乙乘景区观光车时y与x之间的函数关系式为y=kx+b(k≠0),将(20,0),(30,3000)代入y=kx+b得: ![]() ,解得:
,解得: ![]() ,∴乙乘景区观光车时y与x之间的函数关系式为y=300x﹣6000(20≤x≤30).
,∴乙乘景区观光车时y与x之间的函数关系式为y=300x﹣6000(20≤x≤30).
(3)甲步行的速度为:5400÷90=60(米/分),∴甲步行y与x之间的函数关系式为y=60x.
联立两函数关系式成方程组, ![]() ,解得:
,解得: ![]() ,∴甲出发25分钟与乙第一次相遇.
,∴甲出发25分钟与乙第一次相遇.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC=45°.
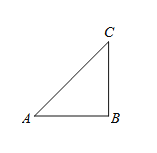
(1)尺规作图:
①在CA的延长线上截取AD=AB,并连结BD;
②在∠BAC内部作∠CAE=∠ABD,交BC边于点E;(保留作图痕迹,不写作法)
(2)求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
(Ⅰ)求△ABC的面积;
(Ⅱ)在图中作出△ABC关于![]() 轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.
轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃容器高20cm,底面圆的周长为48cm,在外侧距下底1cm的点A处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇,则蜘蛛捕获苍蝇所走的最短路线长度为( ).
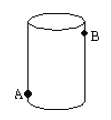
A. 30cmB. 25cmC. ![]() D. 以上答案均不正确
D. 以上答案均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点![]() ,
,![]() ,
,![]() 表示的数分别为1,
表示的数分别为1,![]() ,-3.观察数轴,与点
,-3.观察数轴,与点![]() 的距离为3的点表示的数是____,
的距离为3的点表示的数是____,![]() ,
,![]() 两点之间的距离为_____.
两点之间的距离为_____.
(2)数轴上,点![]() 关于点
关于点![]() 的对称点表示的数是_____.
的对称点表示的数是_____.
(3)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则与
点重合,则与![]() 点重合的点表示的数是_____;若此数轴上
点重合的点表示的数是_____;若此数轴上![]() ,
,![]() 两点之间的距离为2019(
两点之间的距离为2019(![]() 在
在![]() 的左侧),且当
的左侧),且当![]() 点与
点与![]() 点重合时,
点重合时,![]() 点与
点与![]() 点也恰好重合,则点
点也恰好重合,则点![]() 表示的数是_____,点
表示的数是_____,点![]() 表示的数是_____;
表示的数是_____;
(4)若数轴上![]() ,
,![]() 两点间的距离为
两点间的距离为![]() (
(![]() 在
在![]() 左侧),表示数
左侧),表示数![]() 的点到
的点到![]() ,
,![]() 两点的距离相等,将数轴折叠,当
两点的距离相等,将数轴折叠,当![]() 点与
点与![]() 点重合时,点
点重合时,点![]() 表示的数是_____,点
表示的数是_____,点![]() 表示的数是_____(用含
表示的数是_____(用含![]() ,
,![]() 的式子表示这两个数).
的式子表示这两个数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某校举办秋季运动会,七(1)班和七(2)班进行拔河比赛,比赛规定标志物红绸向某班方向移动![]() 或
或![]() 以上,该班就获胜.红绸先向(2)班移动
以上,该班就获胜.红绸先向(2)班移动![]() ,后又向(1)班移动
,后又向(1)班移动![]() ,相持几秒后,红绸向(2)班移动
,相持几秒后,红绸向(2)班移动![]() ,随后又向(1)班移动
,随后又向(1)班移动![]() ,在一片欢呼声中,红绸再向(1)班移动
,在一片欢呼声中,红绸再向(1)班移动![]() ,裁判员一声哨响,比赛结束,请你用计算的方法说明最终获胜的是几班;
,裁判员一声哨响,比赛结束,请你用计算的方法说明最终获胜的是几班;
(2)已知![]() 、
、![]() 互为相反数,
互为相反数,![]() 、
、![]() 互为倒数,
互为倒数,![]() 的绝对值为2,求
的绝对值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
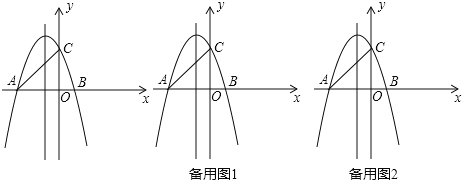
(1)求抛物线的解析式;
(2)点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如4=22﹣02,12=42﹣22,20=62﹣42,因此 4,12,20 都是“神秘数”,则下面哪个数是“神秘数”( )
A.56B.60C.62D.88
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com