
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点![]() ,
,![]() ,
,![]() 表示的数分别为1,
表示的数分别为1,![]() ,-3.观察数轴,与点
,-3.观察数轴,与点![]() 的距离为3的点表示的数是____,
的距离为3的点表示的数是____,![]() ,
,![]() 两点之间的距离为_____.
两点之间的距离为_____.
(2)数轴上,点![]() 关于点
关于点![]() 的对称点表示的数是_____.
的对称点表示的数是_____.
(3)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则与
点重合,则与![]() 点重合的点表示的数是_____;若此数轴上
点重合的点表示的数是_____;若此数轴上![]() ,
,![]() 两点之间的距离为2019(
两点之间的距离为2019(![]() 在
在![]() 的左侧),且当
的左侧),且当![]() 点与
点与![]() 点重合时,
点重合时,![]() 点与
点与![]() 点也恰好重合,则点
点也恰好重合,则点![]() 表示的数是_____,点
表示的数是_____,点![]() 表示的数是_____;
表示的数是_____;
(4)若数轴上![]() ,
,![]() 两点间的距离为
两点间的距离为![]() (
(![]() 在
在![]() 左侧),表示数
左侧),表示数![]() 的点到
的点到![]() ,
,![]() 两点的距离相等,将数轴折叠,当
两点的距离相等,将数轴折叠,当![]() 点与
点与![]() 点重合时,点
点重合时,点![]() 表示的数是_____,点
表示的数是_____,点![]() 表示的数是_____(用含
表示的数是_____(用含![]() ,
,![]() 的式子表示这两个数).
的式子表示这两个数).
【答案】(1)-2或4;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]() ;
;![]() ;(3)
;(3)![]() ;
;![]()
【解析】
(1)根据数轴即可求出与点![]() 的距离为3的点表示的数,然后根据数轴上两点之间的距离公式计算即可;
的距离为3的点表示的数,然后根据数轴上两点之间的距离公式计算即可;
(2)根据数轴上两点的中点公式计算即可;
(3)根据数轴上两点的中点公式即可求出对称中心所表示的数,从而求出结论;
(4)设点![]() 表示的数是p,则点Q表示的数为p+a,再根据中点公式列出等式即可求出结论.
表示的数是p,则点Q表示的数为p+a,再根据中点公式列出等式即可求出结论.
解:(1)由数轴可知:点![]() 的距离为3的点表示的数是-2或4;
的距离为3的点表示的数是-2或4;![]() ,
,![]() 两点之间的距离为1-
两点之间的距离为1-![]() =
=![]()
故答案为:-2或4;![]() ;
;
(2)点![]() 关于点
关于点![]() 的对称点表示的数是2×1-
的对称点表示的数是2×1-![]() =
=![]()
故答案为:![]() ;
;
(3)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则此时对称中心所表示的数为
点重合,则此时对称中心所表示的数为![]()
则与![]() 点重合的点表示的数是2×(-1)-
点重合的点表示的数是2×(-1)-![]() =
=![]() ;
;
∵此数轴上![]() ,
,![]() 两点之间的距离为2019(
两点之间的距离为2019(![]() 在
在![]() 的左侧),
的左侧),
∴设M点所表示的数为m,则N点所表示是数为m+2019
∵当![]() 点与
点与![]() 点重合时,
点重合时,![]() 点与
点与![]() 点也恰好重合,
点也恰好重合,
∴![]()
解得:m=![]()
∴M点所表示的数为![]() ,则N点所表示是数为m+2019=
,则N点所表示是数为m+2019=![]()
故答案为:![]() ;
;![]() ;
;![]()
(4)∵数轴上![]() ,
,![]() 两点间的距离为
两点间的距离为![]() (
(![]() 在
在![]() 左侧),
左侧),
∴设点![]() 表示的数是p,则点Q表示的数为p+a
表示的数是p,则点Q表示的数为p+a
∵表示数![]() 的点到
的点到![]() ,
,![]() 两点的距离相等,
两点的距离相等,
∴![]()
解得:p=![]() ,即点
,即点![]() 表示的数是
表示的数是![]()
∴点Q表示的数为![]() .
.
故答案为:![]() ;
;![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】用一个长方形的纸片制作一个无盖的长方体盒子,设这个长方形的长为a,宽为b,这个无盖的长方体盒子高为c,![]() 只考虑如图所示,在长方形的右边两个角上各剪去一个大小相同的正方形,左上角剪去一个长方形的情况
只考虑如图所示,在长方形的右边两个角上各剪去一个大小相同的正方形,左上角剪去一个长方形的情况![]() 若
若![]() ,则这个无盖长方体盒子的容积是______.
,则这个无盖长方体盒子的容积是______.
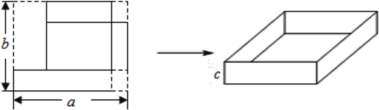
查看答案和解析>>
科目:初中数学 来源: 题型:
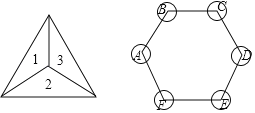
【题目】图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点C处的概率是
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
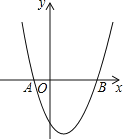
【题目】如图,已知抛物线y=x2-2x-3与x轴交于A、B两点.
(1)当0<x<3时,求y的取值范围;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
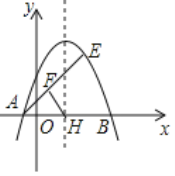
【题目】如图,抛物线y=﹣(x﹣1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).
(1)求抛物线的解析式;
(2)抛物线的对称轴与x轴的交于点是H,点F是AE中点,连接FH.求线段FH的长;
(3)P为直线AE上方抛物线上的点.当△AEP的面积最大时.求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.

(1)乙步行的速度为_ __米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数字﹣1,﹣2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 ;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果,并求出点P(x,y)落在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
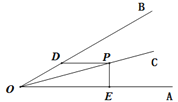
【题目】如图,∠AOB=30°,OC平分∠AOB,P为OC上任意一点,PD∥OA交OB于D,PE⊥OA于E,若OD=4,则PE= __________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com