
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG=_____.

科目:初中数学 来源: 题型:
【题目】已知实数a、b、c满足a+b=ab=c,有下列结论:
①若c≠0,则![]() ;②若a=3,则b+c=9;
;②若a=3,则b+c=9;
③若a=b=c,则abc=0;④若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 (把所有正确结论的序号都选上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)在这次调查中,一共调查了 名市民.
(2)扇形统计图中,C组对应的扇形圆心角是 .
(3)请补全条形统计图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从![]() 两地同时出发,相向而行.快车到达
两地同时出发,相向而行.快车到达![]() 地后,停留3秒卸货,然后原路返回
地后,停留3秒卸货,然后原路返回![]() 地,慢车到达
地,慢车到达![]() 地即停运休息,如图表示的是两车之间的距离
地即停运休息,如图表示的是两车之间的距离![]() (米)与行驶时间
(米)与行驶时间![]() (秒)的函数图象,根据图象信息,计算
(秒)的函数图象,根据图象信息,计算![]() 的值分别为( )
的值分别为( )
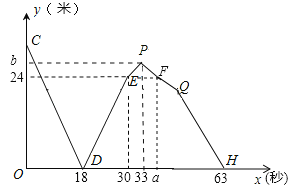
A. 39,26B. 39,26.4C. 38,26D. 38,26.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是合同三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1),若运动方向相反,则称它们是镜面合同三角形(如图2),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°.下列各组合同三角形中,是镜面合同三角形的是( )
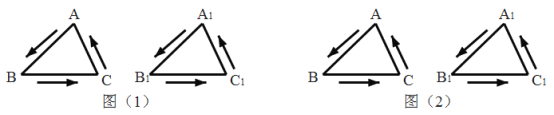
A.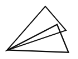 B.
B.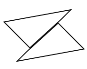 C.
C.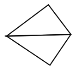 D.
D.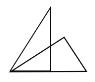
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如,图中三角形ABC是格点三角形,其中S=2,N=0,L=6.

(1)图中格点多边形DEFGHI所对应的S= ,N= ,L= .
(2)经探究发现,任意格点多边形的面积S可表示为S=aN+bL﹣1,其中a,b为常数
①试求a,b的值.(提示:列方程组)
②求当N=5,L=14时,S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
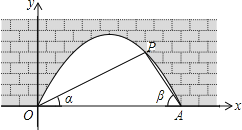
【题目】图中是抛物线拱桥,P处有一照明灯,点P到水面OA的距离为![]() ,从O、A两处观测P处,仰角分别为
,从O、A两处观测P处,仰角分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为
,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为![]() .
.
![]() 求抛物线方程,并求抛物线上的最高点到水面的距离;
求抛物线方程,并求抛物线上的最高点到水面的距离;
![]() 水面上升1m,水面宽多少
水面上升1m,水面宽多少![]() 取
取![]() ,结果精确到
,结果精确到![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com