
【题目】如图所示,O为一个模拟钟面圆心,M、O、N 在一条直线上,指针 OA、OB 分别从 OM、ON 出发绕点 O 转动,OA 运动速度为每秒 30°,OB 运动速度为每秒10°,当一根指针与起始位置重合时,运动停止,设转动的时间为 t 秒,试解决下列问题:
(1)如图①,若OA顺时针转动,OB逆时针转动,![]() = 秒时,OA与OB第一次重合;
= 秒时,OA与OB第一次重合;
(2)如图②,若OA、OB同时顺时针转动,
①当![]() =3秒时,∠AOB= °;
=3秒时,∠AOB= °;
②当![]() 为何值时,三条射线OA、OB、ON其中一条射线是另两条射线夹角的角平分线?
为何值时,三条射线OA、OB、ON其中一条射线是另两条射线夹角的角平分线?



【答案】(1)4.5;(2)① 120°;②经过4.5,7.2秒时,其中一条射线是另外两条射线夹角的平分线.
【解析】
(1)设t秒后第一次重合.根据题意,列出方程,解方程即可;
(2)①利用180°减去OA转动的角度,加上OB转动的角度,即可得到答案;
②先用t的代数式表示∠BON和∠AON,然后分为三种情况进行讨论:当ON、OA、OB为角平分线时,分别求出t的值,即可得到答案.
解:(1)若OA顺时针转动,OB逆时针转动,
∴∠AOM+∠BON=180°,
∴![]() ,
,
解得:![]() ;
;
∴![]() 秒,OA与OB第一次重合;
秒,OA与OB第一次重合;
故答案为:4.5;
(2)①若OA、OB同时顺时针转动,
∴![]() ,
,![]() ,
,
∴![]() ;
;
故答案为:120;
② 由题意知![]() ,
,
∴∠BON=10t ,∠AON=180-30t (0≤t≤6),∠AON=30t-180(6<t≤12).
当ON为∠AOB的角平分线时,有
180-30t =10t ,
解得:t =4.5;
当OA为∠BON的角平分线时,
10t =2(30t -180),
解得:t =7.2;
当OB为∠AON的角平分线时,
30t -180=2×10t ,
解得:t =18(舍去);
∴经过4.5,7.2秒时,射线OA、OB、ON其中一条射线是另外两条射线夹角的平分线.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 的对称轴为直线
的对称轴为直线![]() ,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②a-b+c<0;③当x<1时,y随x增大而增大;
④抛物线的顶点坐标为(2,b);⑤若ax2+bx+c=b,则b2-4ac=0.
其中正确的是( )

A. ①②③ B. ①④⑤ C. ①②④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下4个图中,不同的矩形ABCD,若把D点沿AE对折,使D点与BC上的F点重合;
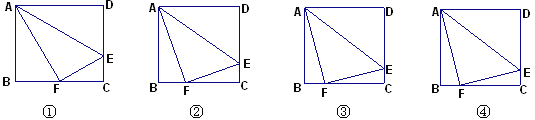
(1)图①中,若DE︰EC=2︰1,求证:△ABF∽△AFE∽△FCE;并计算BF︰FC;
(2)图②中若DE︰EC=3︰1,计算BF︰FC= ;图③中若DE︰EC=4︰1,计算BF︰FC= ;
(3)图④中若DE︰EC=![]() ︰1,猜想BF︰FC= ;并证明你的结论
︰1,猜想BF︰FC= ;并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.
(1)当E与F不重合时,四边形DEBF是平行四边形吗?说明理由;
(2)点 E,F在AC上运动过程中,以D、E、B、F为顶点的四边形是否可能为矩形?如能,求出此时的运动时间t的值;如不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
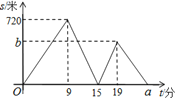
【题目】小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
①小华先到达青少年宫;②小华的速度是小明速度的2.5倍;③a=24;④b=480.其中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的顶点O在坐标原点,顶点A的坐标为(4,3).
(1)顶点![]() 的坐标为( , );
的坐标为( , );
(2)现有动点P、Q分别从C、A同时出发,点P沿线段CB向终点B运动,速度为每秒1个单位,点Q沿折线A→O→C向终点C运动,速度为每秒k个单位,当运动时间为2秒时,以P、Q、C为顶点的三角形是等腰三角形,求此时k的值.
(3)若正方形OABC以每秒![]() 个单位的速度沿射线AO下滑,直至顶点C落到
个单位的速度沿射线AO下滑,直至顶点C落到![]() 轴上时停止下
轴上时停止下
滑.设正方形OABC在![]() 轴下方部分的面积为S,求S关于滑行时间
轴下方部分的面积为S,求S关于滑行时间![]() 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量![]() 的取值范围.
的取值范围.


(备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完。设分配给甲店A型产品x件,两商店销售这两种产品每件的利润(元)如下表:
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1)分配给乙店B型产品 件(用含x的代数式表示)。
(2)设这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并直接写出x的取值范围。
(3)若公司要求总利润不低于17560元,有几种不同分配方案?哪种方案总利润最大?请求出最大利润。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小高从家骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间x(分钟)与离家距离y(千米)的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家需要的时间是_______分钟.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com