
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M.则下列结论:①∠AME=90°,②∠BAF=∠EDB,③AM=![]() MF,④ME+MF=
MF,④ME+MF=![]() MB.其中正确结论的有( )
MB.其中正确结论的有( )
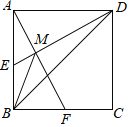
A.4个B.3个C.2个D.1个
【答案】B
【解析】
根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,得出①正确;根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=![]() MF,判断出③正确;过点M作MN⊥AB于N,由相似三角形的性质得出
MF,判断出③正确;过点M作MN⊥AB于N,由相似三角形的性质得出![]() ,解得MN=
,解得MN=![]() a,AN=
a,AN=![]() a,得出NB=AB﹣AN=2a﹣
a,得出NB=AB﹣AN=2a﹣![]() a=
a=![]() a,根据勾股定理得BM=
a,根据勾股定理得BM=![]() a,求出ME+MF=
a,求出ME+MF=![]() +
+![]() =
=![]() a,
a,![]() MB=
MB=![]() a,得出ME+MF=
a,得出ME+MF=![]() MB,故④正确.于是得到结论.
MB,故④正确.于是得到结论.
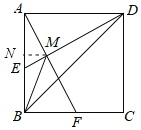
解:在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°,
∵E、F分别为边AB,BC的中点,
∴AE=BF=![]() BC,
BC,
在△ABF和△DAE中,
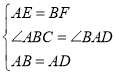 ,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=∠BAD=90°,
∴∠ADE+∠DAF=∠BAD=90°,
∴∠AMD=180°﹣(∠ADE+∠DAF)=180°﹣90°=90°,
∴∠AME=180°﹣∠AMD=180°﹣90°=90°,
故①正确;
∵DE是△ABD的中线,
∴∠ADE≠∠EDB,
∴∠BAF≠∠EDB,
故②错误;
设正方形ABCD的边长为2a,则BF=a,
在Rt△ABF中,![]() ,
,
∵∠BAF=∠MAE,∠ABC=∠AME=90°,
∴△AME∽△ABF,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
故③正确;
如图,过点M作MN⊥AB于N,
则MN∥BC,
∴△AMN∽△AFB,
∴![]() ,
,
即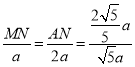 ,
,
解得![]() ,
,![]() ,
,
∴![]() ,
,
根据勾股定理得: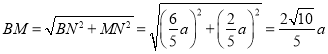 ,
,
∵ME+MF=![]() +
+![]() =
=![]() a,
a,![]() MB=
MB=![]() a,
a,
∴ME+MF=![]() MB,
MB,
故④正确.
综上所述,正确的结论有①③④共3个.
故选:B.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
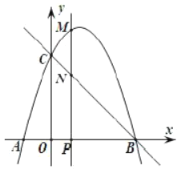
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .动点
.动点![]() 在
在![]() 轴上运动,过点
轴上运动,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
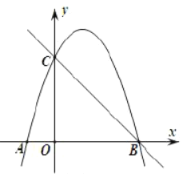
(1)直接写出抛物线的解析式__________和直线![]() 的解析式_________;
的解析式_________;
(2)当点![]() 在线段
在线段![]() 上运动时,直接写出线段
上运动时,直接写出线段![]() 长度的最大值_________;
长度的最大值_________;
(3)当点![]() 在线段
在线段![]() 上运动时,若
上运动时,若![]() 是以
是以![]() 为腰的等腰直角三角形时,求
为腰的等腰直角三角形时,求![]() 的值;
的值;
(4)当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,求出
为顶点的四边形是平行四边形时,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
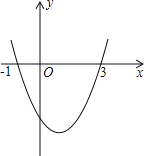
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地之间的路程为3000m,甲、乙两人分别从A、B两地同时出发,相向而行,甲到B地停止,乙到A地停止,出发10分钟后,甲原路原速返回A地取重要物品,取到该物品后立即原路原速前往B地(取物品的时间忽略不计),结果到达B地的时间比乙到达A地的时间晚,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(m)与甲运动的时间x(min)之间的关系如图所示,则乙到达A地时,甲与B地相距的路程是_____m.
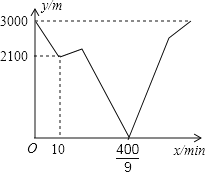
查看答案和解析>>
科目:初中数学 来源: 题型:
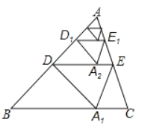
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第1次操作,
处,称为第1次操作,![]() 到折痕
到折痕![]() 的距离记为
的距离记为![]() ;还原纸片后,再将
;还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第2次操作,
处,称为第2次操作,![]() 到折痕
到折痕![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去,经过第2019次操作后,
;按上述方法不断操作下去,经过第2019次操作后,![]() 到折痕
到折痕![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为_____,表示“D等级”的扇形的圆心角为_____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水坝的横截面是梯形![]() ,迎水坡
,迎水坡![]() 的坡角
的坡角![]() 为
为![]() ,背水坡
,背水坡![]() 的坡度
的坡度![]() 为
为![]() ,坝顶宽
,坝顶宽![]() 米,坝高5米.求:
米,坝高5米.求:
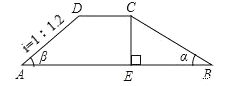
(1)坝底宽![]() 的长(结果保留根号);
的长(结果保留根号);
(2)在上题中,为了提高堤坝的防洪能力,市防汛指挥部决定加固堤坝,要求坝顶![]() 加宽0.5米,背水坡
加宽0.5米,背水坡![]() 的坡度改为
的坡度改为![]() ,已知堤坝的总长度为
,已知堤坝的总长度为![]() ,求完成该项工程所需的土方(结果保留根号).
,求完成该项工程所需的土方(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,分别是两棵树及其影子的情形
(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形.
(2)请画出图中表示小丽影长的线段.
(3)阳光下小丽影子长为1.20m树的影子长为2.40m,小丽身高1.88m,求树高.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com