
����Ŀ����֪������y��ax2+��3b+1��x+b��3��a��0����������ʵ��m��ʹ�õ�P��m��m���ڸ��������ϣ����dzƵ�P��m��m��������������ϵ�һ������г������
��1����a��2��b��1ʱ����������ߵ�����г������
��2������������ʵ��b���������Ϻ���������ͬ������г����A��B��
����ʵ��a��ȡֵ��Χ��
������A��B����ֱ��y����x����![]() +1���Գƣ���ʵ��b����Сֵ��
+1���Գƣ���ʵ��b����Сֵ��
���𰸡���1����![]() ����2����2������2����0��a��27��b����Сֵ��
����2����2������2����0��a��27��b����Сֵ��![]()
��������
��1����x=y=m��a=2��b=1���뺯������ʽ���г����̣�ͨ���ⷽ�����m��ֵ���ɣ�
��2���������Ϻ���������ͬ������г����A��B�������m�ķ���m=am2+��3b+1��m+b-3�ĸ����б�ʽ��=9b2-4ab+12a��
����y=9b2-4ab+12a����������ʵ��b������y��0�����Ը��ݶ��κ���y=9b2-4ab+12��ͼ�����ʽ��
�����ö��κ���ͼ��ĶԳ����ʽ�ɣ�
��1����a��2��b��1ʱ��m��2m2+4m+1��4��
���m��![]() ��m����2��
��m����2��
���Ե�P�������ǣ�![]() ��
��![]() ����2����2����
����2����2����
��2��m��am2+��3b+1��m+b��3��
����9b2��4ab+12a��
����y��9b2��4ab+12a����������ʵ��b������y��0��Ҳ����˵������y��9b2��4ab+12��ͼ����b�ᣨ���ᣩ�Ϸ���
���������4a��2��4��9��12a��0��
��0��a��27��
������������������A��x1��y1����B��x2��y2����
��x1��x2��ax2+��3b+1��x+b��3��0��������ʵ����![]() ��
��
���߶�AB���е������ǣ�����![]() ����
����![]() ��������Գ���y��x����
��������Գ���y��x����![]() +1������
+1������
��![]() ��
��![]() ����
����![]() +1����
+1����
��3b+1��![]() +a��
+a��
��a��0��![]() ��0��a
��0��a![]() ��1Ϊ��ֵ��
��1Ϊ��ֵ��
��3b+1��![]() +a��2
+a��2![]() ��2��
��2��
��b��![]() ��
��
��b����Сֵ��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��1��0����B��1��a��0����C��1+a��0����a��0������P����D��4��4��ΪԲ�ģ�1Ϊ�뾶��Բ���˶�����ʼ�������BPC=90������a����Сֵ��_____��
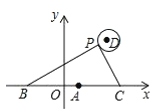
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ��������![]() �У�
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ����
����![]() ��
Ϊ��![]() �ϵ�����һ��(�����
�ϵ�����һ��(�����![]() ��
��![]() �غ�)����
�غ�)����![]() ��
��![]() �۵�������
�۵�������![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ����
����![]() �ı���ʱ��
�ı���ʱ��![]() �ij�Ϊ________.
�ij�Ϊ________.
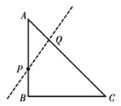
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������1�������2��������Щ�����ɫ�ⶼ��ͬ.
������Ӻ������������1����������ɫ��ĸ���Ϊ_____________��
�����Ӻ������������һ��������ɫ��Żأ��ٴ����������һ������ͨ���б�����״ͼ�ķ�����������������ͬ��ɫ��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OABC�Ķ���O��B��y���ϣ�����A�ڷ���������y����![]() �ϣ�����C�ڷ���������y��
�ϣ�����C�ڷ���������y��![]() �ϣ���OABC������ǣ�������
�ϣ���OABC������ǣ�������
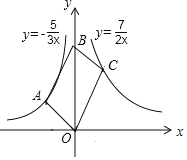
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() Ϊ˫����
Ϊ˫����![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ��
��![]() �ᡢ
�ᡢ![]() ��Ĵ��ߣ��ֱ�ֱ��
��Ĵ��ߣ��ֱ�ֱ��![]() �ڵ�
�ڵ�![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() �·�.��ֱ��
�·�.��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ����
����![]() ��ֵΪ________.
��ֵΪ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�з���5�������Σ���B1��y���ϣ���C1��E1��E2��C2��E3��E4��C3��x���ϣ���������A1B1C1D1�ı߳�Ϊ1����B1C1O��60��B1C1��B2C2��B3C3�����A3��x��ľ����ǣ� ��
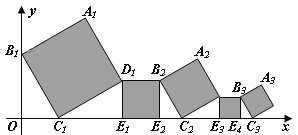
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC���������������ֱ�ΪA(3,3)��B(��1,0)��C(4,0)��
(1)����ƽ�ƣ���ʹ��ABC�Ķ���A������ԭ��O�غϣ���ֱ��д����ʱ��C�Ķ�Ӧ��C1���ꣻ(���ػ���ƽ�ƺ��������)
(2)����ABC�Ƶ�B��ʱ����ת90�㣬�õ���A��BC�䣬������A��BC�䲢д��A�������ꣻ
(3)�Ե�AΪλ�����ķŴ��ABC���õ���AB2C2��ʹ�Ŵ�ǰ������֮��Ϊ1��4�������������ڻ�����A2B2C2.
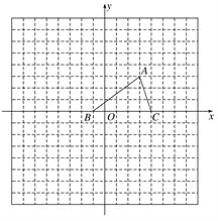
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѱ˸���ȫ��ͬ��С��ƽ��Ϊ���飬ÿ����ÿ���ֱ�д��1��2��3��4�ĸ����֣�Ȼ��ֱ�װ�벻���Ŀڴ��ڽ��ȣ��ӵ�һ���ڴ���ȡ��һ�����������ֺ���Ϊ��P�ĺ�����x��Ȼ���ٴӵڶ����ڴ���ȡ��һ����������ֺ���Ϊ��P�������꣬���P��x��y������ֱ��y=��x+5�ϵĸ����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com