
分析 (1)根据题意可以列出相应的二元一次方程组,解方程组即可求得A、B两种型号的汽车每辆多少万元;
(2)根据第二问提供的信息和第一问中求得的A、B两种型号的汽车每辆多少万元,可以列出一个不等式组,解不等式组即可求得A的取值范围,从而得到相应的购买方案;
(3)根据第二问求得购买方案,分别算出各种方案获得的利润,进行比较,即可求得问题的答案.
解答 解:(1)设A种型号的汽车每辆x万元,B种型号的汽车每辆y万元
$\left\{\begin{array}{l}{3x+5y=111}\\{6x+8y=192}\end{array}\right.$,
解得x=12,y=15.
即A种型号的汽车每辆12万元,B种型号的汽车每辆15万元;
(2)设该经销商购进A种型号的汽车x辆,B种型号的汽车(50-x)辆
$\left\{\begin{array}{l}{12x+15(50-x)≤650}\\{0<x≤36}\end{array}\right.$,
解得$\frac{100}{3}≤x≤36$,
因此,有三种购买方案:
第一种方案:购买A型号的汽车34辆,B型号的汽车16辆;
第二种方案:购买A型号的汽车35辆,B型号的汽车15辆;
第三种方案:购买A型号的汽车36辆,B型号的汽车14辆.
(3)当选择方案一时,获得的利润是:34×12×15%+16×15×16%=99.6万元;
当选择方案二时,获得的利润是:35×12×15%+15×15×16%=99万元;
当选择方案一时,获得的利润是:36×12×15%+14×15×16%=98.4万元;
故经销商使用方案一可获得最大利润,最大利润是99.6万元.
点评 本题考查一次函数的应用、二元一次方程组的应用、一元一次不等式组的应用,解题的关键是根据题意列出相应的关系式,然后对相应的关系式进行解答.


科目:初中数学 来源: 题型:选择题
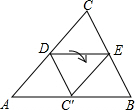 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
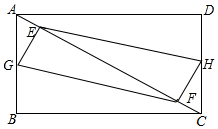 在矩形ABCD中,AB=3,BC=4,E,F是对角线ACS行的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
在矩形ABCD中,AB=3,BC=4,E,F是对角线ACS行的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
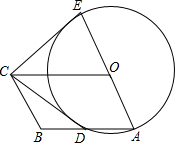 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com