
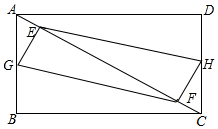
 在矩形ABCD中,AB=3,BC=4,E,F是对角线ACS行的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
在矩形ABCD中,AB=3,BC=4,E,F是对角线ACS行的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.分析 (1)由矩形的性质得出AB=CD,AB∥CD,AD∥BC,∠B=90°,由勾股定理求出AC=5,由SAS证明△AFG≌△CEH,得出GF=HE,同理得出GE=HF,即可得出结论;
(2)先证明四边形BCHG是平行四边形,得出GH=BC=4,当对角线EF=GH=4时,平行四边形EGFH是矩形,分两种情况:①AE=CF=t,得出EF=5-2t=4,解方程即可;②AE=CF=t,得出EF=5-2(5-t)=4,解方程即可;
(3)连接AG、CH,由菱形的性质得出GH⊥EF,OG=OH,OE=OF,得出OA=OC,AG=AH,证出四边形AGCH是菱形,得出AG=CG,设AG=CG=x,则BG=4-x,由勾股定理得出方程,解方程求出BG,得出AB+BG=$\frac{31}{8}$,即可得出t的值.
解答 (1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,∠GAF=∠HCE,
∵G,H分别是AB,DC中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG和△CEH中,$\left\{\begin{array}{l}{AG=CH}&{\;}\\{∠GAF=∠HCE}&{\;}\\{AF=CE}&{\;}\end{array}\right.$,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(2)解:由(1)得:BG=CH,BG∥CH,
∴四边形BCHG是平行四边形,
∴GH=BC=4,当EF=GH=4时,平行四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5-2t=4,
解得:t=0.5;
②AE=CF=t,EF=5-2(5-t)=4,
解得:t=4.5;
综上所述:当t为0.5s或4.5s时,四边形EGFH为矩形.
(3)解: 连接AG、CH,如图所示:
连接AG、CH,如图所示:
∵四边形EGFH为菱形,
∴GH⊥EF,OG=OH,OE=OF,
∴OA=OC,AG=AH,
∴四边形AGCH是菱形,
∴AG=CG,
设AG=CG=x,则BG=4-x,
由勾股定理得:AB2+BG2=AG2,
即32+(4-x)2=x2,
解得:x=$\frac{25}{8}$,
∴BG=4-$\frac{25}{8}$=$\frac{7}{8}$,
∴AB+BG=3+$\frac{7}{8}$=$\frac{31}{8}$,
即t为$\frac{31}{8}$s时,四边形EGFH为菱形.
点评 本题是四边形综合题目,考查了矩形的性质、全等三角形的判定与性质、平行四边形的判定、菱形的判定与性质、勾股定理等知识;本题综合性强,难度较大,特别是(3)中,需要通过作辅助线证明四边形是菱形,运用勾股定理得出方程才能得出结果.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com