
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
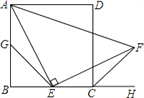
(1)证明:△AGE≌△ECF;
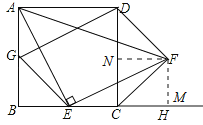
(2)连接GD,DF.判断四边形GEFD的形状,并说明理由;
【答案】(1)详见解析; (2)平行四边形
【解析】(1)证明:∵正方形ABCD,点G,E为边AB、BC中点,∴AG=EC,△BEG为等腰直角三角形,∴∠AGE=180°﹣45°=135°,又∵CF为正方形外角平分线,∴∠ECF=90°+45°=135°,∵∠AEF=90°,∴∠GAE=90°﹣∠AEB=∠CEF,在△AGE和△ECF中,∵∠AGE=∠ECF,AG=CE,∠GAE=∠CEF,∴△AGE≌△ECF(ASA);
(2)四边形GEFD是平行四边形,理由如下:过点F作FM⊥BH于M,过F作FN⊥DC于N,易证△AGD≌△ABE,∴GD=AE,∠BAE=∠ADG,∵△AGE≌△ECF,∴AE=EF,∴GD=EF,在△AGD和△EFM中,∵∠DAG=∠FHE=90°,∠ADG=∠FEH,GD=FE,∴△AGD≌△EFM(AAS),∴GD=EF,在△DFN和△BGE中,∵DN=BE,∠DNF=∠B=90°,NF=BG,∴△DFN≌△BGE( SAS),∴DF=GE,∴四边形GEFD是平行四边形.


科目:初中数学 来源: 题型:
【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去) .
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
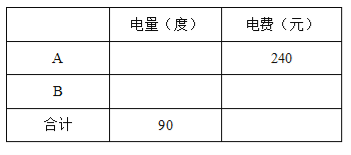
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到 “分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
【解决问题】
解:由题意,得![]() 三个有理数都为正数或其中一个为正数,另两个为负数.
三个有理数都为正数或其中一个为正数,另两个为负数.
①![]() 都是正数,即
都是正数,即![]() 时,则
时,则![]() ;
;
②当![]() 中有一个为正数,另两个为负数时,不妨设
中有一个为正数,另两个为负数时,不妨设![]() ,则
,则![]() .
.
综上所述, ![]() 值为3或-1.
值为3或-1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数![]() 满足
满足![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为三个不为0的有理数,且
为三个不为0的有理数,且![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲜花饼是云南的特色小吃,也是中国四大月饼流派滇式月饼的经典代表之一,深受人们喜爱.现某车间要为鲜花饼制作长方体包装盒,已知一个盒子由一个盒身和两个盒底构成,每一张纸板可以做盒身10个或盒底30个.现有纸板100张,应用多少张制作盒身,多少张制作盒底,才能使盒身和盒底正好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的一个游戏:
口袋中有编号分别为1、2、3的红球三个和编号为4的白球一个,四个球除了颜色或编号不同外,没有任何别的区别,摸球之前将小球搅匀,摸球的人都蒙上眼睛.先甲摸两次,每次摸出一个球;把甲摸出的两个球放回口袋后,乙再摸,乙只摸一个球.如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分;如果乙摸出的球是白色,乙得1分,否则,乙得0分 ;得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图求甲得1分的概率;
(2)这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】气魄雄伟的大礼堂座落在渝中区学田湾,它是一座仿古民族建筑.“五一”期间,小明和妈妈到重庆大礼堂参观游玩.参观结束后,穿过人民广场到达A处,回望礼堂,更显气势雄伟,金碧辉煌.此时,在A点观察到礼堂顶端的仰角为30°,沿着坡度为1:3的斜坡AB走一段距离到达B点,观察到礼堂顶端 的仰角是22°,测得点A与BC之间的水平距离![]() 米,则大礼堂的高度DE为( )米.(精确到1米.参考数据:
米,则大礼堂的高度DE为( )米.(精确到1米.参考数据: ![]() ,
, ![]() .)
.)
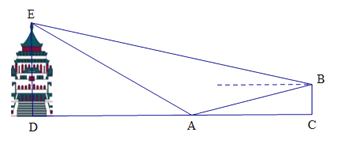
A. 58 B. 60 C. 62 D. 64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是( )

A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com