
| 3 |
| m-4 |
| m-4 |
| 3 |
| 3 |
| m-4 |
| 3 |
| 3 |
| 3 |
| m-4 |
| 3 |
| m-4 |
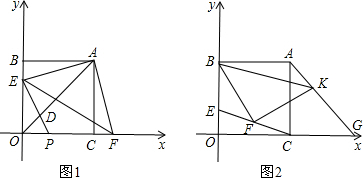
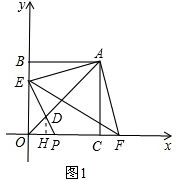 过点D作DH⊥x轴于点H,如图1.
过点D作DH⊥x轴于点H,如图1.| 2 |
| AB2+BE2 |
| 50 |
| 2 |
| 2 |
| 2 |
| OH |
| OC |
| DH |
| AC |
| OD |
| OA |
| OH |
| 7 |
| DH |
| 7 |
2
| ||
7
|
| PH |
| OP |
| DH |
| OE |
| PH |
| 2+PH |
| 2 |
| 7-1 |
| 1 |
| 3 |
|
|
| m-4 |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
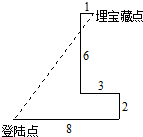 暑假中,小明和同学们到某海岛去探宝旅游,按照如图所示的路线探宝.他们登陆后先往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北走6km处往东一拐,仅走1km就找到了宝藏,则登陆点到埋宝藏点的直线距离为
暑假中,小明和同学们到某海岛去探宝旅游,按照如图所示的路线探宝.他们登陆后先往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北走6km处往东一拐,仅走1km就找到了宝藏,则登陆点到埋宝藏点的直线距离为查看答案和解析>>
科目:初中数学 来源: 题型:
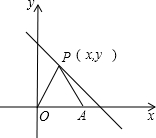 如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6上的点,点A(5,0),O是坐标原点,△PAO的面积为S.
如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6上的点,点A(5,0),O是坐标原点,△PAO的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:
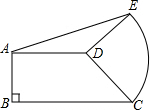 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=4,将腰CD以点D为旋转中心,逆时针方向旋转90°至点E,连接AE,请求出△ADE的面积.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=4,将腰CD以点D为旋转中心,逆时针方向旋转90°至点E,连接AE,请求出△ADE的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com