
【题目】函数y=kx+b和函数y=ax+m的图像如图所示,求下列不等式(组)的解集
(1) kx+b <ax+m的解集是
(2)![]() 的解集是
的解集是
(3)![]() 的解集是
的解集是
(4)![]() 的解集是
的解集是
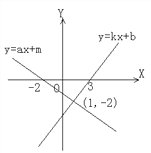
【答案】(1)x<1 (2)x<-2(3)x>3 (4)-2<x<3
【解析】试题分析:根据两个函数的图象位置关系解答;
试题解析:
(1)kx+b <ax+m即函数y=kx+b的图象在函数y=ax+m图象下方对应自变量x的取值范围,由图可得x<1;
(2) ![]() 的解集即为y=kx+b的图象在x轴的下方和函数y=ax+m的图像在x轴的上方应x的取值范围,由图可得x<-2;
的解集即为y=kx+b的图象在x轴的下方和函数y=ax+m的图像在x轴的上方应x的取值范围,由图可得x<-2;
(3) ![]() 的解集即为y=kx+b的图象在x轴的上方和函数y=ax+m的图像在x轴的下方应x的取值范围,由图可得x>3;
的解集即为y=kx+b的图象在x轴的上方和函数y=ax+m的图像在x轴的下方应x的取值范围,由图可得x>3;
(3) ![]() 的解集即为y=kx+b的图象在x轴的下方和函数y=ax+m的图像在x轴的下方应x的取值范围,由图可得-2<x<3;
的解集即为y=kx+b的图象在x轴的下方和函数y=ax+m的图像在x轴的下方应x的取值范围,由图可得-2<x<3;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
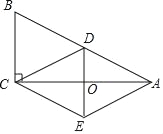
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形.
(2)BC=6,AB=10,求菱形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数m、n,定义一种运算“※”为:m※n=mn+n.
(1)求2※5与2※(﹣5)的值;
(2)如果关于x的方程x※(a※x)=﹣![]() 有两个相等的实数根,求实数a的值.
有两个相等的实数根,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米)
(参考数据:sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
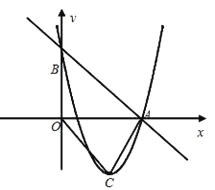
【题目】如图,在直角坐标平面内,直线y=-x+5与![]() 轴和
轴和![]() 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y=![]() +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且![]() ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
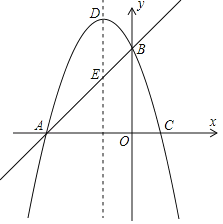
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
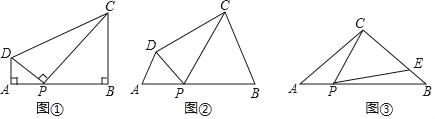
【题目】(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)求证:△DAP~△PBC.
(2)若PD=5,PC=10,BC=9,求AP的长.
(应用)如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com