
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
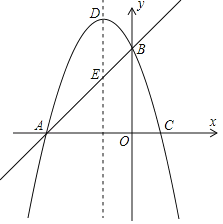
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
【答案】(1)y=﹣x2﹣2x+3
(2)点F的坐标为(![]() ,
,![]() )
)
(3)当t为![]() 秒或2秒或3秒或
秒或2秒或3秒或![]() 秒时,以P、B、C为顶点的三角形是直角三角形。
秒时,以P、B、C为顶点的三角形是直角三角形。
【解析】
试题(1)先由直线AB的解析式为y=x+3,求出它与x轴的交点A、与y轴的交点B的坐标,再将A、B两点的坐标代入y=﹣x2+bx+c,运用待定系数法即可求出抛物线的解析式。
∵y=x+3与x轴交于点A,与y轴交于点B,
∴当y=0时,x=﹣3,即A点坐标为(﹣3,0),当x=0时,y=3,即B点坐标为(0,3)。
将A(﹣3,0),B(0,3)代入y=﹣x2+bx+c,得
![]() ,解得
,解得![]() 。
。
∴抛物线的解析式为y=﹣x2﹣2x+3。
(2)设第三象限内的点F的坐标为(m,﹣m2﹣2m+3),运用配方法求出抛物线的对称轴及顶点D的坐标,再设抛物线的对称轴与x轴交于点G,连接FG,根据S△AEF=S△AEG+S△AFG﹣S△EFG=3,列出关于m的方程,解方程求出m的值,进而得出点F的坐标。
如图1,设第三象限内的点F的坐标为(m,﹣m2﹣2m+3),

则m<0,﹣m2﹣2m+3<0。
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴对称轴为直线x=﹣1,顶点D的坐标为(﹣1,4)。
设抛物线的对称轴与x轴交于点G,连接FG,
则G(﹣1,0),AG=2。
∵直线AB的解析式为y=x+3,
∴当x=﹣1时,y=﹣1+3=2。∴E点坐标为(﹣1,2)。
∵S△AEF=S△AEG+S△AFG﹣S△EFG
=![]() ×2×2+
×2×2+![]() ×2×(m2+2m﹣3)﹣
×2×(m2+2m﹣3)﹣![]() ×2×(﹣1﹣m)=m2+3m,
×2×(﹣1﹣m)=m2+3m,
∴以A、E、F为顶点的三角形面积为3时,m2+3m=3,
解得m1=![]() ,m2=
,m2=![]() (舍去)。
(舍去)。
当m=![]() 时,﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m=
时,﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m=![]() 。
。
∴点F的坐标为(![]() ,
,![]() )。
)。
(3)设P点坐标为(﹣1,n),.
∵B(0,3),C(1,0),∴BC2=12+32=10。
分三种情况:
①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,

即(0+1)2+(n﹣3)2+10=(1+1)2+(n﹣0)2,
化简整理得6n=16,解得n=![]() 。
。
∴P点坐标为(﹣1,![]() )。
)。
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣![]() =
=![]() 。
。
∵点P的速度为每秒1个单位长度,∴t1=![]() 秒。
秒。
②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,

即(0+1)2+(n﹣3)2+(1+1)2+(n﹣0)2=10,
化简整理得n2﹣3n+2=0,解得n=2或1。
∴P点坐标为(﹣1,2)或(﹣1,1),
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣2=2或PD=4﹣1=3。
∵点P的速度为每秒1个单位长度,∴t2=2秒,t3=3秒。
③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,

即10+(1+1)2+(n﹣0)2=(0+1)2+(n﹣3)2,
化简整理得6n=﹣4,解得n=![]() 。
。
∴P点坐标为(﹣1,![]() )。
)。
∵顶点D的坐标为(﹣1,4),∴PD=4+![]() =
=![]() 。
。
∵点P的速度为每秒1个单位长度,
∴t4=![]() 秒。
秒。
综上所述,当t为![]() 秒或2秒或3秒或
秒或2秒或3秒或![]() 秒时,以P、B、C为顶点的三角形是直角三角形。
秒时,以P、B、C为顶点的三角形是直角三角形。


科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:
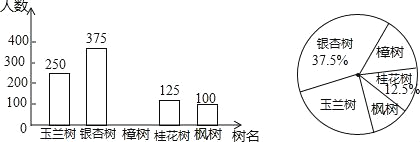
请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
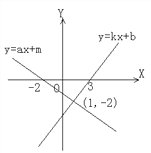
【题目】函数y=kx+b和函数y=ax+m的图像如图所示,求下列不等式(组)的解集
(1) kx+b <ax+m的解集是
(2)![]() 的解集是
的解集是
(3)![]() 的解集是
的解集是
(4)![]() 的解集是
的解集是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商场经销一种高档水果,如果每千克盈利![]() 元,每天可售出
元,每天可售出![]() 千克.经市场调查发现,出售价格每降低
千克.经市场调查发现,出售价格每降低![]() 元,日销售量将增加
元,日销售量将增加![]() 千克.那么每千克应降价多少元,销售该水果每天可获得最大利润?最大利润是多少元?
千克.那么每千克应降价多少元,销售该水果每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为420米,求这栋楼的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
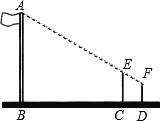
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=﹣x2+4x﹣3,把抛物线C1先向右平移3个单位长度,再向上平移3个单位长度,得到抛物线C2 ,将抛物线C1和抛物线C2这两个图象在x轴及其上方的部分记作图象M.若直线y=kx+ ![]() 与图象M至少有2个不同的交点,则k的取值范围是________.
与图象M至少有2个不同的交点,则k的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com