练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线C1：y=﹣x2+4x﹣3，把抛物线C1先向右平移3个单位长度，再向上平移3个单位长度，得到抛物线C2 ，将抛物线C1和抛物线C2这两个图象在x轴及其上方的部分记作图象M．若直线y=kx+ 与图象M至少有2个不同的交点，则k的取值范围是________．

    【答案】0≤k＜

    【解析】

    首先配方得出二次函数顶点式，求得抛物线C1的顶点坐标，进而利用二次函数平移规律得出抛物线C2，求得顶点坐标，把两点顶点坐标代入即可求得．

    y=﹣x2+4x﹣3=+1，

    ∴抛物线C1的顶点(2,1)

    则将抛物线y=﹣x2+4x﹣3先向右平移3个单位长度，再向上平移3个单位长度，

    得到的新的抛物线C2的解析式为：y=+4.

    ∴抛物线C2顶点(5,4)，

    把(2,1)代入y=kx+ (k0)得,1=2k+，

    解得k=，

    把(5,4)代入y=kx+ (k0)得,4=5k+ ，

    解得k= ，

    ∴直线y=kx+ (k0)与图象M至少有2个不同的交点,则k的取值范围是0k<.

    故答案为：0k<.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，抛物线y=﹣x2+bx+c经过A、B两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．

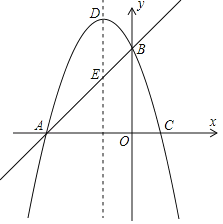
    （1）求抛物线的解析式；

    （2）在第三象限内，F为抛物线上一点，以A、E、F为顶点的三角形面积为3，求点F的坐标；

    （3）点P从点D出发，沿对称轴向下以每秒1个单位长度的速度匀速运动，设运动的时间为t秒，当t为何值时，以P、B、C为顶点的三角形是直角三角形？直接写出所有符合条件的t值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

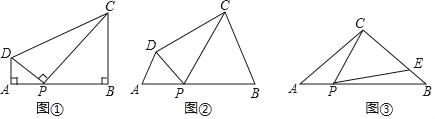
    【题目】（感知）如图①，在四边形ABCD中，点P在边AB上（点P不与点A、B重合），∠A＝∠B＝∠DPC＝90°．易证：△DAP∽△PBC（不要求证明）．

    （探究）如图②，在四边形ABCD中，点P在边AB上（点P不与点A、B重合），∠A＝∠B＝∠DPC．

    （1）求证：△DAP～△PBC．

    （2）若PD＝5，PC＝10，BC＝9，求AP的长．

    （应用）如图③，在△ABC中，AC＝BC＝4，AB＝6，点P在边AB上（点P不与点A、B重合），连结CP，作∠CPE＝∠A，PE与边BC交于点E．当CE＝3EB时，求AP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长为（　　）

    A. B. 5 C. 4 D.

    【答案】B

    【解析】由旋转的性质可知，在图乙中，∠BCE1=15°，∠D1CE1=60°，AB=6，CD1=CD=7，

    ∴∠D1CB=60°-15°=45°，

    又∵∠ACB=90°，

    ∴CO平分∠ACB，

    又∵AC=BC，

    ∴CO⊥AB，且CO=AO=BO=AB=3，

    ∴D1O=CD1-CO=7-3=4，∠AOD1=90°，

    ∴在Rt△AOD1中，AD1=.

    故选B.

    点睛：本题解题的关键是由旋转的性质证明：∠D1CB=45°，从而得到CD1平分∠ACB，结合等腰三角形的“三线合一”证得∠AOD1=90°，并求得AO=3，OD1=4；这样问题就变得很简单了.

    【题型】单选题
    【结束】
    10

    【题目】我市某小区实施供暖改造工程，现甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y（米）与挖掘时间x（天）之间的关系如图所示，则下列说法中，正确的个数有（ ）个．

    ①甲队每天挖100米；

    ②乙队开挖两天后，每天挖50米；

    ③当x=4时，甲、乙两队所挖管道长度相同；

    ④甲队比乙队提前2天完成任务．

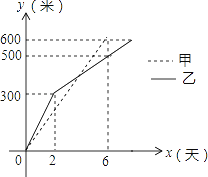
    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四位同学在研究函数y=x2+bx+c(b，c是常数)时，甲发现当x=1时，函数有最小值；乙发现﹣1是方程x2+bx+c=0的一个根；丙发现函数的最小值为3；丁发现当x=2时，y=4，已知这四位同学中只有一位发现的结论是错误的，则该同学是( )

    A. 甲 B. 乙 C. 丙 D. 丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形OABC的边长为2，顶点A，C分别在x轴，y轴的正半轴上，点E是BC的中点，F是AB延长线上一点且FB＝1.

    （1）求经过点O，A，E三点的抛物线解析式；

    （2）点P在抛物线上运动，当点P运动到什么位置时△OAP的面积为2，请求出点P的坐标；

    （3）在抛物线上是否存在一点Q，使△AFQ是等腰直角三角形？若存在直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本小题满分10分）已知二次函数

    （1）当时，函数值随的增大而减小，求的取值范围。

    （2）以抛物线的顶点为一个顶点作该抛物线的内接正三角形（，两点在抛物线上），请问：△的面积是与无关的定值吗？若是，请求出这个定值；若不是，请说明理由。

    （3）若抛物线与轴交点的横坐标均为整数，求整数的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，AD是BC边上的中线.

    (1)画出与△ACD关于点D成中心对称的三角形；

    (2)找出与AC相等的线段；

    (3)探究：△ABC中AB与AC的和与中线AD之间有何大小关系？并说明理由；

    (4)若AB=5，AC=3，求线段AD的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AE是圆O的直径，点B在AE的延长线上，点D在圆O上，且AC⊥DC， AD平分∠EAC

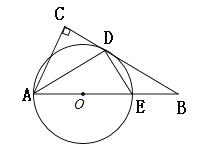
    (1)求证：BC是圆O的切线。

    (2)若BE=8,BD=12,求圆O的半径,

    查看答案和解析>>

    同步练习册答案