
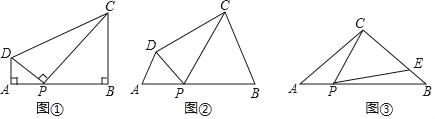
【题目】(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)求证:△DAP~△PBC.
(2)若PD=5,PC=10,BC=9,求AP的长.
(应用)如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
【答案】【探究】(1)证明见解析(2)AP=4.5;【应用】AP=3+![]() 或AP=3﹣
或AP=3﹣![]()
【解析】
探究:(1)根据外角的性质得到∠DPB=∠A+∠ADP,等量代换得到∠ADP=∠CPB,根据相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到![]() ,代入数据即可得到结论;
,代入数据即可得到结论;
应用:根据等腰三角形的性质得到∠A=∠B,根据相似三角形的性质得到ACBE=APBP,代入数据即可得到结论.
探究:(1)∵∠DPB=∠A+∠ADP,
∴∠DPC+∠CPB=∠A+∠ADP,
∵∠A=∠DPC,
∴∠ADP=∠CPB,
∵∠A=∠B,
∴△DAP∽△PBC;
(2)∵△DAP∽△PBC,
∴![]() ,
,
∴![]() ,
,
∴AP=4.5;
应用:∵AC=BC,
∴∠A=∠B,
∵∠CPE=∠A,
∴∠A=∠CPE=∠B,
由探究得△CAP∽△PBE,
∴![]() ,
,
∴ACBE=APBP,
∵BC=4,CE=3EB,
∴BE=1,
∵AC=4,BP=AB﹣AP=6﹣AP,
∴AP(6﹣AP)=4,
∴AP=3+![]() 或AP=3﹣
或AP=3﹣![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
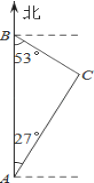
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
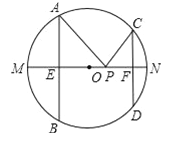
【题目】如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
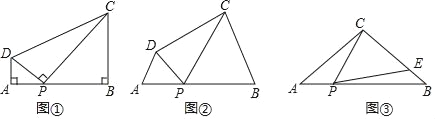
【题目】(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)求证:△DAP~△PBC.
(2)若PD=5,PC=10,BC=9,求AP的长.
(应用)如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
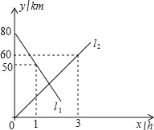
【题目】A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④![]() 小时后两人相遇.
小时后两人相遇.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
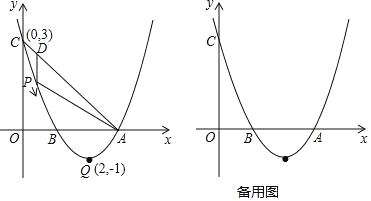
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点 D.
(1)求该抛物线的函数关系式及A、B两点的坐标;
(2)求点P在运动的过程中,线段PD的最大值;
(3)若点P与点Q重合,点E在x轴上,点F在抛物线上,问是否存在以A,P,E,F为顶点的平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,取一根9.5 m长的标杆AB,在其上系一活动旗帜C,使标杆的影子落在平地和一堤坝的左斜坡上,拉动旗帜使其影子正好落在斜坡底角顶点D处.若测得旗高BC=4.5 m,影长BD=9 m,影长DE=5 m,请计算左斜坡的坡比(假设标杆的影子BD,DE均与坝底线DM垂直).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com