
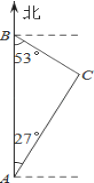
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
【答案】27.5海里/时
【解析】
先过点C作CD⊥AB,垂足为点D,设BD=x海里,得出AD=(99-x)海里,在Rt△BCD中,根据tan53°=![]() ,求出CD,再根据
,求出CD,再根据![]() x=
x=![]() (121-x),求出BD,在Rt△BCD中,根据cos53°=
(121-x),求出BD,在Rt△BCD中,根据cos53°=![]() ,求出BC,从而得出答案.
,求出BC,从而得出答案.
解:如图,根据题意可得,在△ABC中,AB=121海里,∠ABC=53°,∠BAC=27°,点C作CD⊥AB,垂足为点D.
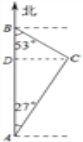
设BD=x海里,则AD=(121﹣x)海里,
在Rt△BCD中,tan53°=![]() ,则tan27°=
,则tan27°=![]() ,
,
CD=xtan53°≈![]() (海里).
(海里).
在Rt△ACD中,则CD=ADtan27°≈![]() (121﹣x),
(121﹣x),
则![]() =
=![]() (121﹣x),
(121﹣x),
解得,x=33, 即BD=33.
在Rt△BCD中,cos53°=![]() ,
,
则BC=![]() =55,
=55,
55÷2=27.5(海里/时),
则该可疑船只的航行速度约为27.5海里/时.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】云南鲁甸6.5级地震后,空军某部奉命赴灾区空投救灾物资,已知物资离开飞机在空中沿抛物线降落,抛物线的顶点在机舱舱口点A处(如图所示).
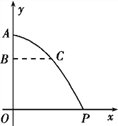
(1)若物体离开A处后下落的竖直高度AB=160 m时,水平距离BC=200 m,那么要使飞机在竖直高度OA=1 km的空中空投的物资恰好落在居民点P处,求飞机到点P处的水平距离OP应为多少;
(2)根据当时的风力测算,空投物资离开A处的竖直距离为160 m时,它到A处的水平距离将增至400 m.要使飞机在(1)中的点O正上方空投物资到P处,飞机离地面的高度应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD的对角线AC、BD相交于点O,AB=6,BC=8,若△AOB是等腰三角形,则平行四边形ABCD的面积等于_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
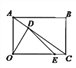
【题目】如图,在矩形ABCO中,AO=3, OC=4,设D、E分别是线段AC、OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动(不包含A、C两个端点).当t=___________时,△ODE为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,下图记录了跑得最快的一位选手与最慢的一位选手的跑步全过程(两人都跑完了全程),其中x代表的是最快的选手全程的跑步时间,y代表的是这两位选手之间的距离,下列说不合理的是()
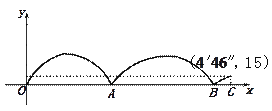
A. 出发后最快的选手与最慢的选手相遇了两次;
B. 出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时短;
C. 最快的选手到达终点时,最慢的选手还有415米未跑;
D. 跑的最慢的选手用时![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com