
【题目】如图,在![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 延长线上,
延长线上,![]() ,
,![]() .
.
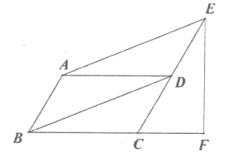
(1)求证:四边形![]() 是平行四边形
是平行四边形
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】探究证明:
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,以
,以![]() 为边在数轴的上方作正方形ABCD.动点
为边在数轴的上方作正方形ABCD.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴正方向匀速运动,同时动点
个单位长度的速度沿数轴正方向匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,到达
匀速运动,到达![]() 点后再以同样的速度沿数轴正方向匀速运动,设运动时间为
点后再以同样的速度沿数轴正方向匀速运动,设运动时间为![]() 秒
秒![]() .
.
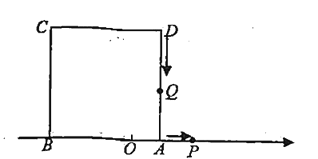
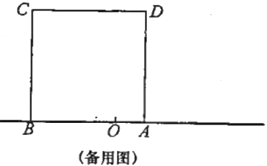
(1)若点![]() 在线段
在线段![]() .上运动,当t为何值时,
.上运动,当t为何值时,![]() ?
?
(2)若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,当t为何值时,三角形
,当t为何值时,三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的
面积的![]() ?
?
(3)在点![]() 和点
和点![]() 运动的过程中,当
运动的过程中,当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 恰好重合?
恰好重合?
(4)当点![]() 在数轴上运动时,是否存在某-时刻t,使得线段
在数轴上运动时,是否存在某-时刻t,使得线段![]() 的长为
的长为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小红开展读书比赛.小明找出了一本以前已读完84页的古典名著打算继续往下读,小红上个周末恰好刚买了同一版本的这本名著,不过还没开始读.于是,两人开始了读书比赛.他们利用下表来记录了两人5天的读书进程.例如,第5天结束时,小明还领先小红24页,此时两人所读到位置的页码之和为424.已知两人各自每天所读页数相同.
读书天数 | 1 | 2 | 3 | 4 | 5 |
页码之差 | 72 | 60 | 48 | 36 | 24 |
页码之和 | 152 | 220 | 424 |
(1)表中空白部分从左到右2个数据依次为 , ;
(2)小明、小红每人每天各读多少页?
(3)已知这本名著有488页,问:从第6天起,小明至少平均每天要比原来多读几页,才能确保第10天结束时还不被小红超过?(答案取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
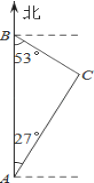
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条高铁线A,B,C三个车站的位置如图所示.已知B,C两站之间相距530千米.高铁列车从B站出发,向C站方向匀速行驶,经过13分钟距A站165千米;经过80分钟距A站500千米.
![]()
(1)求高铁列车的速度和AB两站之间的距离.(2)如果高铁列车从A站出发,开出多久可以到达C站?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题,已知A,B两地相距60千米,甲骑自行车,乙骑摩托车都沿一条笔直的公路由A地匀速行驶到B地,乙每小时比甲多行30千米.甲比乙早出发3小时,乙出发1小时后刚好追上甲.
(1)求甲的速度;
(2)问乙出发之后,到达B地之前,何时甲乙两人相距6千米;
(3)若丙骑自行车与甲同时出发,沿着这条笔直的公路由B地匀速行驶到A地.经过![]() 小时与乙相遇,求此时甲、丙两人之间距离.
小时与乙相遇,求此时甲、丙两人之间距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
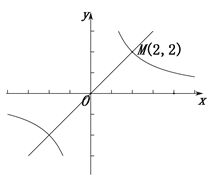
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 与反比例函数
与反比例函数![]() (k≠0)的图象相交于点
(k≠0)的图象相交于点![]() .
.
(1)求k的值;
(2)点![]() 是y轴上一点,过点P且平行于x轴的直线分别与一次函数
是y轴上一点,过点P且平行于x轴的直线分别与一次函数![]() 、反比例函数
、反比例函数![]() 的图象相交于点
的图象相交于点![]() 、
、![]() ,当
,当![]() 时,画出示意图并直接写出a的取值范围.
时,画出示意图并直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com