
【题目】如图,在矩形ABCO中,AO=3, OC=4,设D、E分别是线段AC、OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动(不包含A、C两个端点).当t=___________时,△ODE为直角三角形.
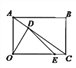
【答案】![]() 或1
或1
【解析】
可分二种情况(①,∠ODE=90°,②∠DEO=90°)讨论,然后只需运用相似三角形的性质就可解决问题.
过点D作DH⊥OC于点H,如图1,
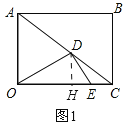
由题可知:AD=3t,CE=t,
∵OC=4,∴OE=OC-EC=4-t,
在Rt△AOC中,
∵∠AOC=90°,OA=3,OC=4,
∴AC=![]() =5.
=5.
∵∠DHC=∠AOC=90°,∠HCD=∠OCA,
∴△HCD∽△OCA,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() ,CH=
,CH=![]() ,
,
∴OH=OC-CH=4-![]() =
=![]() ,
,
①若∠ODE=90°,如图1.
∵DH⊥OC,
∴∠DHO=∠DHE=90°,
∴∠ODH=90°-∠HDE=∠HED,
∴△DHO∽△EHD,
∴![]() ,
,
∴DH2=OHEH,
∴(![]() )2=
)2=![]() (
(![]() -t),
-t),
整理得:19t2-34t+15=0,
解得:t1=1,t2=![]() .
.
②若∠DEO=90°,如图2,
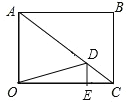
则∠DEC=∠AOC=90°,
∵∠ECD=∠OCA,
∴△DEC∽△AOC,
∴![]() ,
,
∴![]() ,
,
解得:t=![]() .
.
综上所述:当以O、D、E三点为顶点的三角形是直角三角形时,t的值为1、![]() 、
、![]() .
.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数, 从下到上的第![]() 个至第
个至第![]() 个台阶上依次标着
个台阶上依次标着![]() ,且任意相邻四个台阶上的数的和都相等.
,且任意相邻四个台阶上的数的和都相等.

![]() 求前
求前![]() 个台阶上的数的和;
个台阶上的数的和;
![]() 求第
求第![]() 个台阶上的数x的值;
个台阶上的数x的值;
![]() 从下到上前
从下到上前![]() 为奇数)个台阶上的数的和能否为
为奇数)个台阶上的数的和能否为![]() ?若能,求出
?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC和△ABD中,∠DAB=∠ABC=90°,AD=AB=CB,BD=6cm,F为线段BD上一动点,以每秒1cm的速度从B匀速运动到D,过F作直线FQ⊥AF,且FQ=AF,点Q在直线AF的右侧,设点F运动时间为t(s).
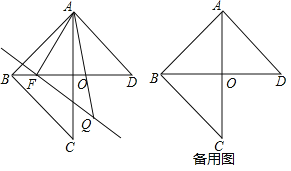
(1)当△ABF为等腰三角形时,t= ;
(2)当F点在线段BO上时,过Q点作QH⊥BD于点H,求证:△AOF≌△FHQ;
(3)当F点在线段OD上运动的过程中,△ABQ的面积是否变化?若不变,求出它的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,以
,以![]() 为边在数轴的上方作正方形ABCD.动点
为边在数轴的上方作正方形ABCD.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴正方向匀速运动,同时动点
个单位长度的速度沿数轴正方向匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,到达
匀速运动,到达![]() 点后再以同样的速度沿数轴正方向匀速运动,设运动时间为
点后再以同样的速度沿数轴正方向匀速运动,设运动时间为![]() 秒
秒![]() .
.
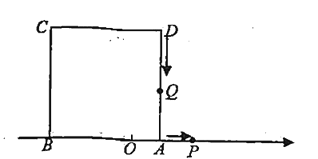
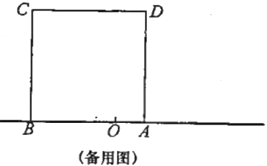
(1)若点![]() 在线段
在线段![]() .上运动,当t为何值时,
.上运动,当t为何值时,![]() ?
?
(2)若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,当t为何值时,三角形
,当t为何值时,三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的
面积的![]() ?
?
(3)在点![]() 和点
和点![]() 运动的过程中,当
运动的过程中,当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 恰好重合?
恰好重合?
(4)当点![]() 在数轴上运动时,是否存在某-时刻t,使得线段
在数轴上运动时,是否存在某-时刻t,使得线段![]() 的长为
的长为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、…、,按一定规律排成如表:
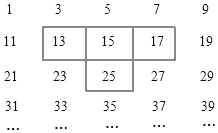
图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数, 若将T字框上下左右移动,则框住的四个数的和不可能得到的数是( )
A.22B.70C.182D.206
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小红开展读书比赛.小明找出了一本以前已读完84页的古典名著打算继续往下读,小红上个周末恰好刚买了同一版本的这本名著,不过还没开始读.于是,两人开始了读书比赛.他们利用下表来记录了两人5天的读书进程.例如,第5天结束时,小明还领先小红24页,此时两人所读到位置的页码之和为424.已知两人各自每天所读页数相同.
读书天数 | 1 | 2 | 3 | 4 | 5 |
页码之差 | 72 | 60 | 48 | 36 | 24 |
页码之和 | 152 | 220 | 424 |
(1)表中空白部分从左到右2个数据依次为 , ;
(2)小明、小红每人每天各读多少页?
(3)已知这本名著有488页,问:从第6天起,小明至少平均每天要比原来多读几页,才能确保第10天结束时还不被小红超过?(答案取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
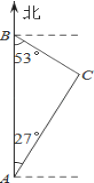
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题,已知A,B两地相距60千米,甲骑自行车,乙骑摩托车都沿一条笔直的公路由A地匀速行驶到B地,乙每小时比甲多行30千米.甲比乙早出发3小时,乙出发1小时后刚好追上甲.
(1)求甲的速度;
(2)问乙出发之后,到达B地之前,何时甲乙两人相距6千米;
(3)若丙骑自行车与甲同时出发,沿着这条笔直的公路由B地匀速行驶到A地.经过![]() 小时与乙相遇,求此时甲、丙两人之间距离.
小时与乙相遇,求此时甲、丙两人之间距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.
![]()
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com