
【题目】已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.

【答案】(1)即圆心O到AQ的距离为4cm;(2)EF=6cm.
【解析】
试题
(1)过点O作OH⊥EF,垂足为点H,求出AO,根据含30度角的直角三角形性质求出即可;
(2)连接OE,根据勾股定理求出EH,根据垂径定理得出即可.
试题解析:
(1)过点O作OH⊥EF,垂足为点H,
∵OH⊥EF,
∴∠AHO=90°,
在Rt△AOH中,∵∠AHO=90°,∠PAQ=30°,
∴OH=![]() AO,
AO,
∵BC=10cm,
∴BO=5cm.
∵AO=AB+BO,AB=3cm,
∴AO=3+5=8cm,
∴OH=4cm,即圆心O到AQ的距离为4cm.
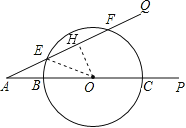
(2)连接OE,
在Rt△EOH中,
∵∠EHO=90°,∴EH2+HO2=EO2,
∵EO=5cm,OH=4cm,
∴EH=![]() =3cm,
=3cm,
∵OH过圆心O,OH⊥EF,
∴EF=2EH=6cm.


科目:初中数学 来源: 题型:
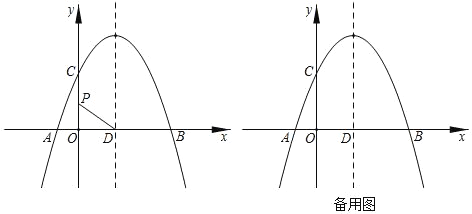
【题目】已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0),且与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求抛物线的解析式;
(2)点P是y轴正半轴上的一个动点,连结DP,将线段DP绕着点D顺时针旋转90°得到线段DE,点P的对应点E恰好落在抛物线上,求出此时点P的坐标;
(3)点M(m,n)是抛物线上的一个动点,连接MD,把MD2表示成自变量n的函数,并求出MD2取得最小值时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
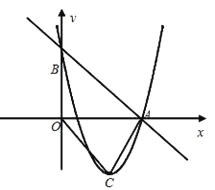
【题目】如图,在直角坐标平面内,直线y=-x+5与![]() 轴和
轴和![]() 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y=![]() +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且![]() ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线与x轴相交于两点A(1,0),B(-3,0),与y轴相交于点C(0,3).
(1)求此抛物线的函数表达式;
(2)如果点![]() 是抛物线上的一点,求△ABD的面积.
是抛物线上的一点,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
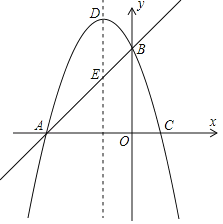
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
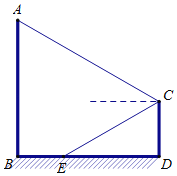
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有编号分别为1、2、3的球(除编号以为,其余都相同),其中1号球1个,3号球3个,从中随机摸出一个球是2号球的概率为![]() .
.
(1)求袋子里2号球的个数.
(2)甲、乙两人分别从袋中摸出一个球(不放回),甲摸出球的编号记为x,乙摸出球的编号记为y,用列表法求点A(x,y)在直线y=x下方的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com