
【题目】已知抛物线与x轴相交于两点A(1,0),B(-3,0),与y轴相交于点C(0,3).
(1)求此抛物线的函数表达式;
(2)如果点![]() 是抛物线上的一点,求△ABD的面积.
是抛物线上的一点,求△ABD的面积.
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
(1)求抛物线的解析式.
(2)若抛物线上有一点P,连PC交线段BM于Q点,且S△BPQ=S△CMQ,求P点的坐标.
(3)把抛物线沿x轴正半轴平移n个单位,使平移后的抛物线交直线BC于E、F两点,且E、F关于点B对称,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() , AD=4.
, AD=4.
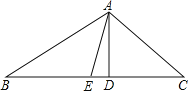
(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB,BC,CD分别与⊙O相切于E,F,G三点,且AB∥CD,连接OB,OC.
(1)如图1,求∠BOC的度数;
(2)如图2,延长CO交⊙O于点M,过点M作MN∥OB交CD于点N,当OB=6,OC=8时,求⊙O的半径及MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
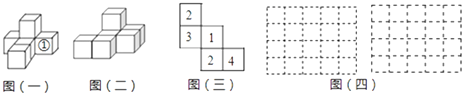
【题目】按要求完成问题:(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
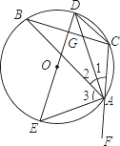
【题目】如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
(1)求证:DE是△ABC的外接圆的直径;
(2)设OG=3,CD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com