
分析 根据二次根式的乘除法,即可解答.
解答 解:(1)$\frac{\sqrt{3}}{\sqrt{5}}=\frac{\sqrt{3}×\sqrt{5}}{\sqrt{5}×\sqrt{5}}=\frac{\sqrt{15}}{5}$;
(2)$\frac{1}{\sqrt{8}}=\frac{1×\sqrt{2}}{\sqrt{2}×\sqrt{8}}=\frac{\sqrt{2}}{4}$;
(3)$\frac{\sqrt{5b}}{\sqrt{12{a}^{3}}}=\frac{\sqrt{5b}×\sqrt{3a}}{\sqrt{12{a}^{3}}×\sqrt{3a}}=\frac{\sqrt{15ab}}{6{a}^{2}}$.
点评 本题考查了二次根式的乘除法,解决本题的关键是熟记二次根式的乘除法.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:填空题
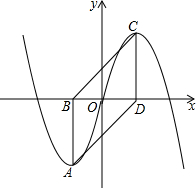 如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.
如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
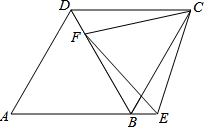 如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:
如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
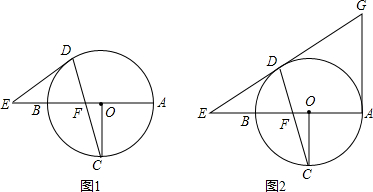
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com