
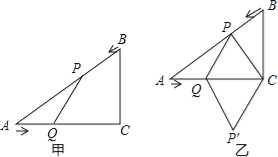
【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?
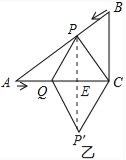
(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′
(3)当t为何值时,△APQ是等腰三角形?
【答案】(1)当t为![]() 秒时,S最大值为
秒时,S最大值为![]() cm2;
cm2;
当四边形PQP′C为菱形时,t的值是s;![]()
当t为![]() s或
s或![]() s或
s或![]() s时,△APQ是等腰三角形.
s时,△APQ是等腰三角形.
【解析】
试题
(1)过点P作PH⊥AC于H,由△APH∽△ABC,得出![]() =
=![]() ,从而求出AB,再根据
,从而求出AB,再根据![]() =
=![]() ,得出PH=3﹣
,得出PH=3﹣![]() t,则△AQP的面积为:
t,则△AQP的面积为:![]() AQPH=
AQPH=![]() t(3﹣
t(3﹣![]() t),最后进行整理即可得出答案;
t),最后进行整理即可得出答案;
(2)连接PP′交QC于E,当四边形PQP′C为菱形时,得出△APE∽△ABC,![]() =
=![]() ,求出AE=﹣
,求出AE=﹣![]() t+4,再根据QE=AE﹣AQ,QE=
t+4,再根据QE=AE﹣AQ,QE=![]() QC得出﹣
QC得出﹣![]() t+4=﹣
t+4=﹣![]() t+2,再求t即可;
t+2,再求t即可;
(3)由(1)知,PD=﹣![]() t+3,与(2)同理得:QD=﹣
t+3,与(2)同理得:QD=﹣![]() t+4,从而求出PQ=
t+4,从而求出PQ=![]() ,/span>
,/span>
在△APQ中,分三种情况讨论:①当AQ=AP,即t=5﹣t,②当PQ=AQ,即![]() =t,③当PQ=AP,即
=t,③当PQ=AP,即![]() =5﹣t,再分别计算即可
=5﹣t,再分别计算即可
试题解析:
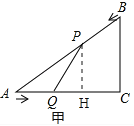
解:(1)如图甲,过点P作PH⊥AC于H,
∵∠C=90°,
∴AC⊥BC,
∴PH∥BC,
∴△APH∽△ABC,
∴![]() =
=![]() ,
,
∵AC=4cm,BC=3cm,
∴AB=5cm,
∴![]() =
=![]() ,
,
∴PH=3﹣![]() t,
t,
∴△AQP的面积为:
S=![]() ×AQ×PH=
×AQ×PH=![]() ×t×(3﹣
×t×(3﹣![]() t)=﹣
t)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t为![]() 秒时,S最大值为
秒时,S最大值为![]() cm2.
cm2.
(2)如图乙,连接PP′,PP′交QC于E,
当四边形PQP′C为菱形时,PE垂直平分QC,即PE⊥AC,QE=EC,
∴△APE∽△ABC,
∴![]() =
=![]() ,
,
∴AE=![]() =
=![]() =﹣
=﹣![]() t+4
t+4
QE=AE﹣AQ═﹣![]() t+4﹣t=﹣
t+4﹣t=﹣![]() t+4,
t+4,
QE=![]() QC=
QC=![]() (4﹣t)=﹣
(4﹣t)=﹣![]() t+2,
t+2,
∴﹣![]() t+4=﹣
t+4=﹣![]() t+2,
t+2,
解得:t=![]() ,
,
∵0<![]() <4,
<4,
∴当四边形PQP′C为菱形时,t的值是![]() s;
s;
(3)由(1)知,
PD=﹣![]() t+3,与(2)同理得:QD=AD﹣AQ=﹣
t+3,与(2)同理得:QD=AD﹣AQ=﹣![]() t+4
t+4
∴PQ=![]() =
=![]() =
=![]() ,
,
在△APQ中,
①当AQ=AP,即t=5﹣t时,解得:t1=![]() ;
;
②当PQ=AQ,即![]() =t时,解得:t2=
=t时,解得:t2=![]() ,t3=5;
,t3=5;
③当PQ=AP,即![]() =5﹣t时,解得:t4=0,t5=
=5﹣t时,解得:t4=0,t5=![]() ;
;
∵0<t<4,
∴t3=5,t4=0不合题意,舍去,
∴当t为![]() s或
s或![]() s或
s或![]() s时,△APQ是等腰三角形.
s时,△APQ是等腰三角形.


科目:初中数学 来源: 题型:
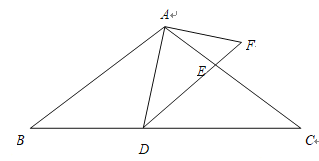
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点(点
边上的一个动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 平分
平分![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
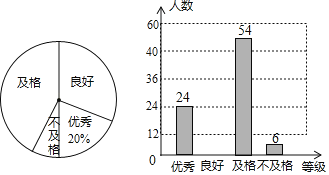
【题目】2019年全国青少年禁毒知识竞赛开始以来,某市青少年学生踊跃参加,掀起了学习禁毒知识的热潮,禁毒知识竞赛的成绩分为四个等级:优秀,良好,及格,不及格.为了了解该市广大学生参加禁毒知识竞赛的成绩,抽取了部分学生的成绩,根据抽查结果,绘制了如下两幅不完整的统计图:
(1)本次抽查的人数是 ;扇形统计图中不及格学生所占的圆心角的度数为 ;
(2)补全条形统计图;
(3)若某校有2000名学生,请你根据调查结果估计该校学生知识竞赛成绩为“优秀”和“良好”两个等级共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
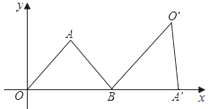
【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,4
,4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
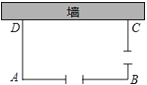
(1)若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
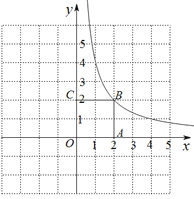
【题目】在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过边长为2的正方形OABC的顶点B,如图,直线
)的图象经过边长为2的正方形OABC的顶点B,如图,直线![]() 与
与![]() (
(![]() )的图象交于点D(点D在直线BC的上方),与x轴交于点E .
)的图象交于点D(点D在直线BC的上方),与x轴交于点E .
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.记![]() (
(![]() )的图象在点B,D之间的部分与线段AB,AE,DE围成的区域(不含边界)为W.
)的图象在点B,D之间的部分与线段AB,AE,DE围成的区域(不含边界)为W.
①当![]() 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;
②若区域W内恰有3个整点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中为真命题的是( )
A.长度为![]() 的三条线段若满足
的三条线段若满足![]() ,则这三条线段一定能组成三角形
,则这三条线段一定能组成三角形
B.一个三角形的三个内角度数之比为3:4:5,则这个三角形是直角三角形
C.正六边形的外角和大于正五边形的外角和
D.若![]() 与
与![]() 相似,且周长相等,则
相似,且周长相等,则![]() 与
与![]() 全等
全等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com