练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列命题中为真命题的是（　　）

    A.长度为的三条线段若满足，则这三条线段一定能组成三角形

    B.一个三角形的三个内角度数之比为3：4：5，则这个三角形是直角三角形

    C.正六边形的外角和大于正五边形的外角和

    D.若与相似，且周长相等，则与全等

    【答案】D

    【解析】

    根据三角形的三边关系、三角形内角和定理、多边形的外角和、相似三角形的性质判断即可．

    解：长度为的三条线段若满足 ＜c＜，则这三条线段一定能组成三角形，A是假命题； 三个内角度数之比为3：4：5， 设三个内角度数分别为3x、4x、5x， 则3x+4x+5x=180°， 解得，x=15°， 则三个内角度数分别为45°、60°、75°， ∴这个三角形是锐角三角形，B是假命题； 正六边形的外角和等于正五边形的外角和，C是假命题； 若△ABC与△DEF相似，且周长相等，则△ABC与△DEF全等，D是真命题；

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

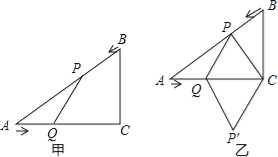
    【题目】如图甲，在△ABC中，∠ACB=90°，AC=4cm，BC=3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连接PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：

    （1）设△APQ的面积为S，当t为何值时，S取得最大值？S的最大值是多少？

    （2）如图乙，连接PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；′

    （3）当t为何值时，△APQ是等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

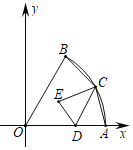
    【题目】如图，扇形OAB中，∠AOB＝60°，OA＝4，点C为弧AB的中点，D为半径OA上一点，点A关于直线CD的对称点为E，若点E落在半径OA上，则OE＝______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了46米木栏．

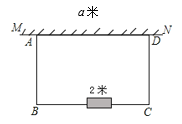
    （1）若a＝26，所围成的矩形菜园的面积为280平方米，求所利用旧墙AD的长；

    （2）求矩形菜园ABCD面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，转盘A中的6个扇形的面积相等，转盘B中的3个扇形的面积相等．分别任意转动转盘A、B各1次，当转盘停止转动时，将指针所落扇形中的2个数字分别作为平面直角坐标系中一个点的横坐标、纵坐标．

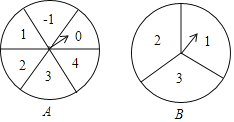
    （1）用表格列出这样的点所有可能的坐标；

    （2）求这些点落在二次函数y＝x2﹣5x+6的图象上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

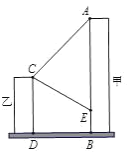
    【题目】我市在创建全国文明城市的过程中，某社区在甲楼的处与处之间悬挂了一幅宣传条幅，在乙楼顶部点测得条幅顶端点的仰角为45°，测得条幅底端点的俯角为30°，若甲、乙两楼之间的水平距离为12米．

    （1）甲楼比乙楼高多少米？

    （2）求条幅AE的长度．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小王电子产品专柜以20元/副的价格批发了某新款耳机，在试销的60天内整理出了销售数据如下

    销售数据(第x天)

    售价(元)

    日销售量(副)

    1≤x＜35

    x+30

    100﹣2x

    35≤x≤60

    70

    100﹣2x

    (1)若试销阶段每天的利润为W元，求出W与x的函数关系式；

    (2)请问在试销阶段的哪一天销售利润W可以达到最大值？最大值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形中，，点从点出发向点移动，速度为每秒1个单位长度，点从点出发向点移动，速度为每秒2个单位长度. 两点同时出发，且其中的任何一点到达终点后，另一点的移动同时停止.

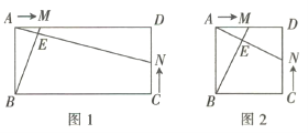
    （1）若两点的运动时间为，当为何值时，？

    （2）在（1）的情况下，猜想与的位置关系并证明你的结论.

    （3）①如图2，当时，其他条件不变，若（2）中的结论仍成立，则_________.

    ②当，时，其他条件不变，若（2）中的结论仍成立，则_________（用含的代数式表示）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，正方形的边长为4，取边上的中点，连接，过点作于点，连接，过点作于点，交于点，交于点，则________．

    查看答案和解析>>

    同步练习册答案