
【题目】已知如图,正方形![]() 的边长为4,取
的边长为4,取![]() 边上的中点
边上的中点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ________.
________.
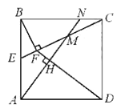
【答案】1
【解析】
如图,延长DF交AB于P.首先证明EF:CF=1:4,由△ADP≌△BAN,推出BN=AP,DP=AM,由PE∥DC,推出PE:DC=EF:CF=1:4,推出PE=BP=1,再证明∠NCM=∠NMC即可解决问题;
解:如图,延长DF交AB于P.
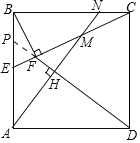
∵四边形ABCD是正方形, ∴AD=AB,∠ABN=∠DAP=90°,
∵AN⊥DP, ∴∠APD+∠PAH=90°,∠ANB+∠PAH=90°,
∴∠APD=∠ANB, ∴△ADP≌△BAN,
∴AN=DP,
∵BF⊥EC, ∴∠EBF+∠BEF=90°,∠BCE+∠BEC=90°,
∴∠EBF=∠BCE, ∴tan∠EBF=tan∠BCE=![]() ,
,
∵AB=BC,BE=AE, ∴tan∠EBF=tan∠BCE= ![]() ,
,
设EF=a,则BF=2a,CF=4a,
∵PE∥DC, ∴![]() ,
,
∵CD=4, ∴PE=1, ∵BE=2, ∴PE=PB=1,
∴PF=![]() BE=1,AP=3,
BE=1,AP=3,
在Rt△ADP中,![]() ,
,
∴DF=4,BN=AP=3,CN=1, ∴BC=DF, ∴∠DFC=∠DCF,
∵∠BCE+∠DCF=90°,∠FMH+∠DFC=90°,∠FMH=∠NMC,
∴∠NCM=∠NMC, ∴MN=CN=1.
故答案为1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列命题中为真命题的是( )
A.长度为![]() 的三条线段若满足
的三条线段若满足![]() ,则这三条线段一定能组成三角形
,则这三条线段一定能组成三角形
B.一个三角形的三个内角度数之比为3:4:5,则这个三角形是直角三角形
C.正六边形的外角和大于正五边形的外角和
D.若![]() 与
与![]() 相似,且周长相等,则
相似,且周长相等,则![]() 与
与![]() 全等
全等
查看答案和解析>>
科目:初中数学 来源: 题型:
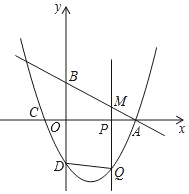
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
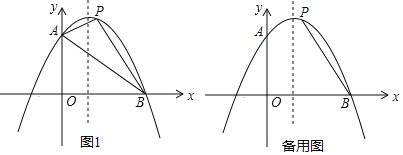
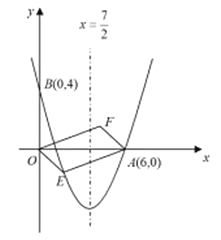
【题目】如图1,已知抛物线y=ax2+2x+c(a≠0),与y轴交于点A(0,6),与x轴交于点B(6,0).
(1)求这条抛物线的表达式及其顶点坐标;
(2)设点P是抛物线上的动点,若在此抛物线上有且只有三个P点使得△PAB的面积是定值S,求这三个点的坐标及定值S.
(3)若点F是抛物线对称轴上的一点,点P是(2)中位于直线AB上方的点,在抛物线上是否存在一点Q,使得P、Q、B、F为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线经过点
的抛物线经过点![]() 和
和![]() .
.
(1)求抛物线解析式;
(2)设点![]() 是抛物线上一动点,且位于第四象限,四边形
是抛物线上一动点,且位于第四象限,四边形![]() 是以
是以![]() 为对角线的平行四边形.
为对角线的平行四边形.
①求平行四边形![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当平行四边形![]() 的面积为24时,请判断平行四边形
的面积为24时,请判断平行四边形![]() 是否为菱形?
是否为菱形?
③是否存在点![]() ,使平行四边形
,使平行四边形![]() 为正方形?若存在,求出点
为正方形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
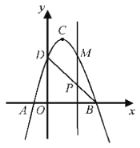
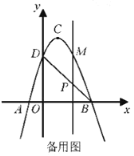
(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴垂线,交抛物线于点
轴垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 、
、![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高
边上的高![]() ?若存在求出点
?若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奇异果是新西兰的特产,其实它的祖籍在中国,又名“猕猴桃”.2018年1月份至6月份我市某大型超市新西兰品种的奇异果销售价格y(元/盒)与月份x(1≤x≤6,且x为整数)之间的函数关系如下表:

7月份至12月份奇异果的销售价格y(元/盒)与月份x之间满足函数关系式:y=2x+20(7≤x≤12且x为整数).该超市去年奇异果销售数量z(盒)与月份x(1≤x≤12,且x为整数)之间存在如图所示的变化趋势.若去年该超市奇异果的进价为每盒20元,销售奇异果需要一名超市员工,该员工每月固定人工费用为1500元.
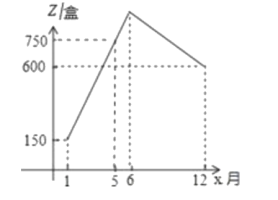
(1)请观察图表中的数据信息直接写出2018年1月份至6月份销售价格y与x之间的函数关系式__ ,根据如图所示的变化趋势,直接写出去年每月销售数量z与x之间满足的函数关系式__ .
(2)求出去年每月该超市的利润w(元)与月份x之间满足的函数关系式.(利润=收入成本费用)
(3)从今年1月份开始,超市决定每卖出一盒奇异果,公司向希望工程捐款2元,奇异果的进价为每盒26元,虽然今年1月份奇异果的销售价格比去年12月份增加4元,但1月份销售数量仍比去年12月份增加了0.4a%;2月份销售价格在1月份的基础上增加了0.5a%,由于其它水果陆续上市,2月份的销售量与1月份持平,这样2月份的利润达到了15780元,请参考以下数据,求出整数a的值.(参考数据:![]() =2025,
=2025,![]() =2116,
=2116,![]() =2209)
=2209)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com