
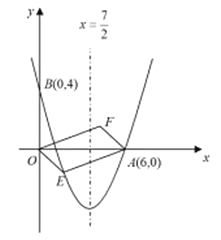
【题目】如图,对称轴为直线![]() 的抛物线经过点
的抛物线经过点![]() 和
和![]() .
.
(1)求抛物线解析式;
(2)设点![]() 是抛物线上一动点,且位于第四象限,四边形
是抛物线上一动点,且位于第四象限,四边形![]() 是以
是以![]() 为对角线的平行四边形.
为对角线的平行四边形.
①求平行四边形![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当平行四边形![]() 的面积为24时,请判断平行四边形
的面积为24时,请判断平行四边形![]() 是否为菱形?
是否为菱形?
③是否存在点![]() ,使平行四边形
,使平行四边形![]() 为正方形?若存在,求出点
为正方形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ,
,![]() ,②当点E为(4,-4)时,平行四边形OEAF不是菱形;当点E为(3,-4)时,平行四边形OEAF是菱形.③不存在这样的点
,②当点E为(4,-4)时,平行四边形OEAF不是菱形;当点E为(3,-4)时,平行四边形OEAF是菱形.③不存在这样的点![]() ,使平行四边形
,使平行四边形![]() 是正方形,理由见解析.
是正方形,理由见解析.
【解析】
(1)将抛物线解析式设成顶点式,然后用待定系数法就可解决问题.
(2)①求出抛物线与x轴的交点坐标,就可得到x的取值范围,由于△OAE与△AOF全等,因此S=2S△OAE=-6y,然后把y换成x的代数式即可.
②易求出点E的纵坐标y,从而求出点E的坐标,然后算出OE、AE的长,就可判定四边形OEAF是否为菱形;
③可先求出使四边形OEAF是菱形时点E的坐标,然后再验证菱形OEAF是否是正方形.
解:(1)由抛物线的对称轴是![]() ,可设解析式为
,可设解析式为![]() .
.
把![]() 、
、![]() 两点坐标代入上式,得
两点坐标代入上式,得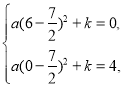
解得:![]() ,
,![]() .
.
∴抛物线的解析式为:![]() .
.
(2)①∵点![]() 在抛物线上,位于第四象限,
在抛物线上,位于第四象限,
∴![]() ,即
,即![]() ,
,![]() 表示点
表示点![]() 到
到![]() 的距离.
的距离.
∵![]() 是
是![]() 的对角线,
的对角线,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
∵抛物线与![]() 轴的两个交点是
轴的两个交点是![]() 和
和![]() ,
,
∴自变量![]() 的取值范围是
的取值范围是![]() ;
;
∴![]() ,(
,(![]() ).
).
②依题意,当![]() 时,即
时,即![]() ,
,
解得![]() ,
,![]() ;
;
Ⅰ.当x=4时,![]() ,则点E(4,-4).
,则点E(4,-4).
过点E作EH⊥x轴,垂足为H,如图2,
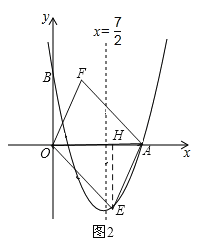
则有OH=4,EH=4,AH=2.
∵EH⊥x轴,
∴OE=![]() ,AE=
,AE=![]() .
.
∴OE≠AE.
∴平行四边形OEAF不是菱形.
Ⅱ.当x=3时,![]() ,则点E(3,-4).
,则点E(3,-4).
过点E作EH⊥x轴,垂足为H,如图3,
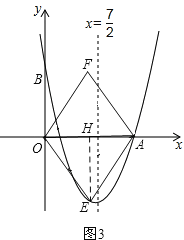
则有OH=3,EH=4,AH=3.
∵EH⊥x轴,
∴OE=5,AE=5.
∴OE=AE.
∴平行四边形OEAF是菱形.
综上所述;当点E为(4,-4)时,平行四边形OEAF不是菱形;当点E为(3,-4)时,平行四边形OEAF是菱形.
③不存在点E,使四边形OEAF为正方形.
理由如下:
当点E在线段OA的垂直平分线上时,EO=EA,则平行四边形OEAF是菱形,如图4,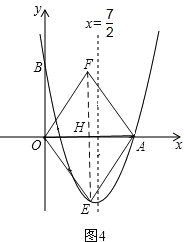
此时,![]() ,
,![]() ,,点E为(3,-4).
,,点E为(3,-4).
则有OA=6,EF=8.
∵OA≠EF,
∴菱形OEAF不是正方形.
∴不存在点E,使四边形OEAF为正方形.


科目:初中数学 来源: 题型:
【题目】如图,转盘A中的6个扇形的面积相等,转盘B中的3个扇形的面积相等.分别任意转动转盘A、B各1次,当转盘停止转动时,将指针所落扇形中的2个数字分别作为平面直角坐标系中一个点的横坐标、纵坐标.
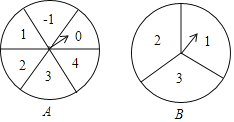
(1)用表格列出这样的点所有可能的坐标;
(2)求这些点落在二次函数y=x2﹣5x+6的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】向阳中学为了解全校学生利用课外时间阅读的情况,调查者随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表(图).根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整;
(3)阅读时间不低于5小时的6人中,有2名男生、4名女生.现从这6名学生中选取两名同学进行读书宣讲,求选取的两名学生恰好是两名女生的概率.
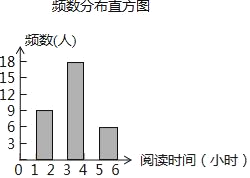
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
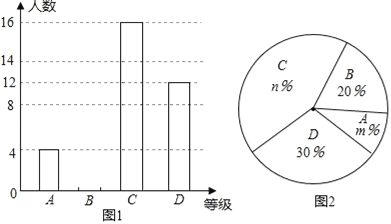
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“精准扶贫”这是新时期党和国家扶贫工作的精髓和亮点.某校团委随机抽取部分学生,对他们是否了解关于“精准扶贫”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如下,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:
(1)求本次活动共调查了 名学生;图1中,B区域的圆心角度是 ;在抽取的学生中调查结果的中位数落在 区域里.
(2)补全条形统计图.
(3)若该校有1200名学生,请估算该校不是了解很多的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
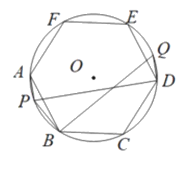
【题目】如图,正六边形ABCDEF内接于⊙O,在弧AB上取点P,连接AP,BP,过点D作DQ∥AP交⊙O于点Q,连接BQ. 已知BP=1,BQ=3,PQ的长为 ,AP的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
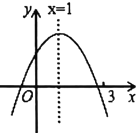
【题目】二次函数![]() 的图象如图所示,有下列结论:①
的图象如图所示,有下列结论:①![]() ;②
;②![]() ;③若
;③若![]() 为任意实数,则
为任意实数,则![]() ;④a-b+c>0;⑤若
;④a-b+c>0;⑤若![]() ,且
,且![]() ,则
,则![]() .其中,正确结论的个数为( )
.其中,正确结论的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com