
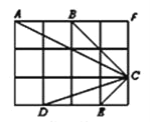
【题目】如图,在![]() 的正方形方格中,
的正方形方格中,![]() 和
和![]() 的顶点都在边长为1的小正方形的顶点上.
的顶点都在边长为1的小正方形的顶点上.
(1)填空:![]() ,
,![]() ;
;
(2)判断![]() 与
与![]() 是否相似,并证明你的结论.
是否相似,并证明你的结论.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
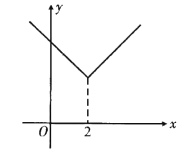
【题目】对于某一函数给出如下定义:对于任意实数![]() ,当自变量
,当自变量![]() 时,函数
时,函数![]() 关于
关于![]() 的函数图象为
的函数图象为![]() ,将
,将![]() 沿直线
沿直线![]() 翻折后得到的函数图象为
翻折后得到的函数图象为![]() ,函数
,函数![]() 的图象由
的图象由![]() 和
和![]() 两部分共同组成,则函数
两部分共同组成,则函数![]() 为原函数的“对折函数”,如函数
为原函数的“对折函数”,如函数![]() (
(![]() )的对折函数为
)的对折函数为![]() .
.
(1)求函数![]() (
(![]() )的对折函数;
)的对折函数;
(2)若点![]() 在函数
在函数![]() (
(![]() )的对折函数的图象上,求
)的对折函数的图象上,求![]() 的值;
的值;
(3)当函数![]() (
(![]() )的对折函数与
)的对折函数与![]() 轴有不同的交点个数时,直接写出
轴有不同的交点个数时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点A为中心,把△ABC逆时针旋转120°,得到△AB'C′(点B、C的对应点分别为点B′、C′),连接BB',若AC'∥BB',则∠CAB'的度数为( )

A.45°B.60°C.70°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
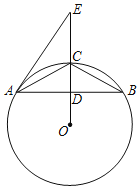
【题目】如图,⊙O为△ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且∠EAC=∠ABC.
(1)求证:直线AE是⊙O的切线.
(2)若D为AB的中点,CD=6,AB=16
①求⊙O的半径;
②求△ABC的内心到点O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年“519(我要走)全国徒步日(江夏站)”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会(活动主办方)为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品![]() 件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
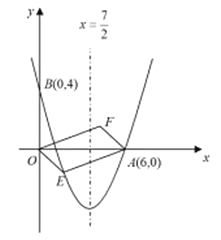
【题目】如图,对称轴为直线![]() 的抛物线经过点
的抛物线经过点![]() 和
和![]() .
.
(1)求抛物线解析式;
(2)设点![]() 是抛物线上一动点,且位于第四象限,四边形
是抛物线上一动点,且位于第四象限,四边形![]() 是以
是以![]() 为对角线的平行四边形.
为对角线的平行四边形.
①求平行四边形![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当平行四边形![]() 的面积为24时,请判断平行四边形
的面积为24时,请判断平行四边形![]() 是否为菱形?
是否为菱形?
③是否存在点![]() ,使平行四边形
,使平行四边形![]() 为正方形?若存在,求出点
为正方形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E为BC边上的一点.连结AE.
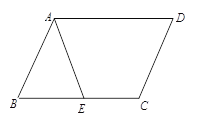
(1)若AB=AE, 求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF︰FA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
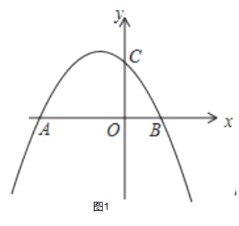
【题目】如图1,二次函数![]() 的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0)
的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0)
(1)b= ,点B的坐标是 ;
(2)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由
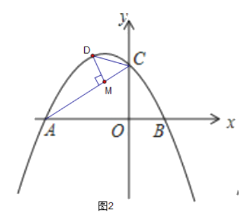
(3)如图2,点D是抛物线上第二象限内的一动点,过点D作DM⊥AC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠BAC的2倍?若存在,写出点D的横坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末上午小明和大强分别从家出发,相约一起去体育馆打球,小明比大强先出发![]() ,大强出发
,大强出发![]() 后与小明相遇.小明的行进速度为
后与小明相遇.小明的行进速度为![]() ,设小明、大强两人相距
,设小明、大强两人相距![]() 与小明行进的时间
与小明行进的时间![]() 之间的函数关系如图所示:
之间的函数关系如图所示:
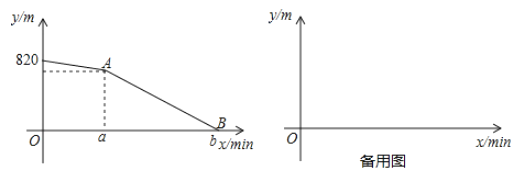
(1)填空:![]() ,小明和大强家相距
,小明和大强家相距 ![]() :
:
(2)求线段![]() 对应的函数表达式,并直接写出自变量
对应的函数表达式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)设大强离家的距离为![]() ,小明行进的时间
,小明行进的时间![]() ,求
,求![]() 与
与![]() 的函数关系式,并画出函数的图象.
的函数关系式,并画出函数的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com