
°æƒø°ø∂‘”⁄ƒ≥“ª∫Ø ˝∏¯≥ˆ»Áœ¬∂®“£∫∂‘”⁄»Œ“‚ µ ˝![]() £¨µ±◊‘±‰¡ø
£¨µ±◊‘±‰¡ø![]() ±£¨∫Ø ˝
±£¨∫Ø ˝![]() πÿ”⁄
πÿ”⁄![]() µƒ∫Ø ˝ÕºœÛŒ™
µƒ∫Ø ˝ÕºœÛŒ™![]() £¨Ω´
£¨Ω´![]() —ÿ÷±œþ
—ÿ÷±œþ![]() ∑≠’€∫Ûµ√µΩµƒ∫Ø ˝ÕºœÛŒ™
∑≠’€∫Ûµ√µΩµƒ∫Ø ˝ÕºœÛŒ™![]() £¨∫Ø ˝
£¨∫Ø ˝![]() µƒÕºœÛ”…
µƒÕºœÛ”…![]() ∫Õ
∫Õ![]() ¡Ω≤ø∑÷π≤Õ¨◊È≥…£¨‘Ú∫Ø ˝
¡Ω≤ø∑÷π≤Õ¨◊È≥…£¨‘Ú∫Ø ˝![]() Œ™‘≠∫Ø ˝µƒ°∞∂‘’€∫Ø ˝°±£¨»Á∫Ø ˝
Œ™‘≠∫Ø ˝µƒ°∞∂‘’€∫Ø ˝°±£¨»Á∫Ø ˝![]() (
(![]() )µƒ∂‘’€∫Ø ˝Œ™
)µƒ∂‘’€∫Ø ˝Œ™![]() .
.
(1)«Û∫Ø ˝![]() (
(![]() )µƒ∂‘’€∫Ø ˝£ª
)µƒ∂‘’€∫Ø ˝£ª
(2)»Ùµ„![]() ‘⁄∫Ø ˝
‘⁄∫Ø ˝![]() (
(![]() )µƒ∂‘’€∫Ø ˝µƒÕºœÛ…œ£¨«Û
)µƒ∂‘’€∫Ø ˝µƒÕºœÛ…œ£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
(3)µ±∫Ø ˝![]() (
(![]() )µƒ∂‘’€∫Ø ˝”Î
)µƒ∂‘’€∫Ø ˝”Î![]() ÷·”–≤ªÕ¨µƒΩªµ„∏ˆ ˝ ±£¨÷±Ω”–¥≥ˆ
÷·”–≤ªÕ¨µƒΩªµ„∏ˆ ˝ ±£¨÷±Ω”–¥≥ˆ![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
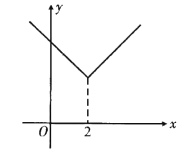
°æ¥∞∏°ø(1)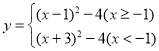 £ª(2)
£ª(2)![]() ªÚ-6£ª(3)n<-1 ±£¨”Îx÷·”–4∏ˆΩªµ„£¨n=-1 ±£¨”Îx÷·”–3∏ˆΩªµ„£ª
ªÚ-6£ª(3)n<-1 ±£¨”Îx÷·”–4∏ˆΩªµ„£¨n=-1 ±£¨”Îx÷·”–3∏ˆΩªµ„£ª![]() ”Îx÷·”–2∏ˆΩªµ„£ªn=3 ±£¨”Îx÷·”–3∏ˆΩªµ„£ªn>3 ±£¨”Îx÷·ŒÞΩªµ„.
”Îx÷·”–2∏ˆΩªµ„£ªn=3 ±£¨”Îx÷·”–3∏ˆΩªµ„£ªn>3 ±£¨”Îx÷·ŒÞΩªµ„.
°æΩ‚Œˆ°ø
£®1£©∏˘æð∂®“µ√≥ˆ∂‘’€∫Û∫Ø ˝µƒ∂•µ„◊¯±ÍŒ™![]() £¨∏√∫Ø ˝±Ì¥Ô ΩŒ™£∫
£¨∏√∫Ø ˝±Ì¥Ô ΩŒ™£∫![]() £ª
£ª
£®2£©Ω´µ„![]() ¥˙»Î
¥˙»Î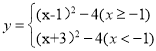 «ÛΩ‚≥ˆmµƒ÷µº¥ø…£ª
«ÛΩ‚≥ˆmµƒ÷µº¥ø…£ª
£®3£©)∑÷µ±![]() ±°¢µ±
±°¢µ±![]() ±°¢ µ±
±°¢ µ±![]() ±°¢µ±
±°¢µ±![]() ±°¢µ±
±°¢µ±![]() ±£¨ª≠≥ˆæþõƒ∫Ø ˝ÕºœÒΩ¯––π€≤Ï”Îx÷·µƒΩªµ„∏ˆ ˝º¥ø…
±£¨ª≠≥ˆæþõƒ∫Ø ˝ÕºœÒΩ¯––π€≤Ï”Îx÷·µƒΩªµ„∏ˆ ˝º¥ø…
(1)¡Ó![]() £¨‘Ú
£¨‘Ú![]() ªÚ3£¨»ÁÕº1£∫º¥µ„
ªÚ3£¨»ÁÕº1£∫º¥µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨
£¨![]() £¨‘Ú∂‘’€∫Û∫Ø ˝µƒ∂•µ„◊¯±ÍŒ™
£¨‘Ú∂‘’€∫Û∫Ø ˝µƒ∂•µ„◊¯±ÍŒ™![]() £¨∏√∫Ø ˝±Ì¥Ô ΩŒ™£∫
£¨∏√∫Ø ˝±Ì¥Ô ΩŒ™£∫![]() £¨
£¨
º¥∂‘’€∫Ø ˝Œ™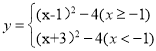 .
.
(2)Ω´µ„![]() ¥˙»Î
¥˙»Î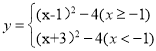
Ω‚µ√£∫![]() ªÚ-6(≤ª∫œÃ‚“‚µƒ÷µ“—…·»•)
ªÚ-6(≤ª∫œÃ‚“‚µƒ÷µ“—…·»•)
º¥![]() ªÚ-6£ª
ªÚ-6£ª
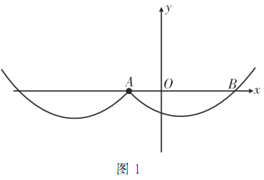
(3)¢Ÿµ±![]() ±£¨»ÁÕº2£∫
±£¨»ÁÕº2£∫
¥À ±![]() ‘⁄µ„
‘⁄µ„![]() µƒ◊Û≤ý£¨¥”Õº÷–ø…“‘ø¥≥ˆ£∫∫Ø ˝”Î
µƒ◊Û≤ý£¨¥”Õº÷–ø…“‘ø¥≥ˆ£∫∫Ø ˝”Î![]() ÷·”–4∏ˆΩªµ„
÷·”–4∏ˆΩªµ„![]() £ª
£ª
¢⁄µ±![]() ±£¨
±£¨![]() π˝µ„
π˝µ„![]() £¨¥”Õº1ø…“‘ø¥≥ˆ£∫∫Ø ˝”Î
£¨¥”Õº1ø…“‘ø¥≥ˆ£∫∫Ø ˝”Î![]() ÷·”–3∏ˆΩªµ„£ª
÷·”–3∏ˆΩªµ„£ª
¢€Õ¨¿Ì£∫µ±![]() ±£¨∫Ø ˝”Î
±£¨∫Ø ˝”Î![]() ÷·”–2∏ˆΩªµ„£ª
÷·”–2∏ˆΩªµ„£ª
¢ÐÕ¨¿Ì£∫µ±![]() ±£¨∫Ø ˝”Î
±£¨∫Ø ˝”Î![]() ÷·”–3∏ˆΩªµ„£ª
÷·”–3∏ˆΩªµ„£ª
¢ðÕ¨¿Ì£∫µ±![]() ±£¨ŒÞΩªµ„.
±£¨ŒÞΩªµ„.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄“ª¥Œœƒ¡Ó”™÷–£¨–°¡¡¥”Œª”⁄![]() µ„µƒ”™µÿ≥ˆ∑¢£¨—ÿ±±∆´∂´60°„∑ΩœÚ◊þ¡À
µ„µƒ”™µÿ≥ˆ∑¢£¨—ÿ±±∆´∂´60°„∑ΩœÚ◊þ¡À![]() µΩ¥Ô
µΩ¥Ô![]() µÿ£¨»ª∫Û‘Ÿ—ÿ±±∆´Œ˜30°„∑ΩœÚ◊þ¡À»Ù∏…«ß√◊µΩ¥Ô
µÿ£¨»ª∫Û‘Ÿ—ÿ±±∆´Œ˜30°„∑ΩœÚ◊þ¡À»Ù∏…«ß√◊µΩ¥Ô![]() µÿ£¨≤‚µ√
µÿ£¨≤‚µ√![]() µÿ‘⁄
µÿ‘⁄![]() µÿƒœ∆´Œ˜30°„∑ΩœÚ£¨‘Ú
µÿƒœ∆´Œ˜30°„∑ΩœÚ£¨‘Ú![]() °¢
°¢![]() ¡Ωµÿµƒæý¿ÎŒ™_________
¡Ωµÿµƒæý¿ÎŒ™_________![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄°—O÷–£¨∞Îæ∂Œ™4£¨œ“ABµƒ≥§Œ™![]() £¨œ“ABÀ˘∂‘µƒ‘≤÷ÐΩ«µƒ∂» ˝Œ™_____________£Æ
£¨œ“ABÀ˘∂‘µƒ‘≤÷ÐΩ«µƒ∂» ˝Œ™_____________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
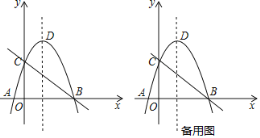
°æƒø°ø»ÁÕº£¨÷±œþy£Ω©Åx+3”Îx÷·°¢y÷·∑÷±Ωª”⁄B°¢C¡Ωµ„£¨≈◊ŒÔœþy£Ω©Åx2+bx+cæ≠π˝B°¢C¡Ωµ„£¨”Îx÷·¡Ì“ªΩªµ„Œ™A£¨∂•µ„Œ™D£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©‘⁄x÷·…œ’““ªµ„E£¨ π°˜EDCµƒ÷Ð≥§◊Ó–°£¨«Û∑˚∫œÃıº˛µƒEµ„◊¯±Í£ª
£®3£©‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ «∑ҥʑ⁄“ªµ„P£¨ πµ√°œAPB£Ω°œOCB£ø»Ù¥Ê‘⁄£¨«Û≥ˆPB2µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y=x2©Å2x©Å1£Æ
x | °≠ | ©Å1 | 0 | 1 | 2 | 3 | °≠ |
y | °≠ | °° °° | °° °° | °° °° | °° °° | °° °° | °≠ |
£®1£©«Î‘⁄±Ìƒ⁄µƒø’∏Ò÷–ÃӻΠµ±µƒ ˝£ª
£®2£©∏˘æ𡖱̣¨«Î‘⁄À˘∏¯µƒ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–ª≠≥ˆy=x2©Å2x©Å1µƒÕºœÛ£ª
£®3£©µ±x‘⁄ ≤√¥∑∂Œßƒ⁄ ±£¨yÀÊx‘ˆ¥Û∂¯ºı–°£ª

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨◊™≈ÃA÷–µƒ6∏ˆ…»–Œµƒ√ʪ˝œýµ»£¨◊™≈ÃB÷–µƒ3∏ˆ…»–Œµƒ√ʪ˝œýµ»£Æ∑÷±»Œ“‚◊™∂Ø◊™≈ÃA°¢B∏˜1¥Œ£¨µ±◊™≈ÃÕ£÷π◊™∂Ø ±£¨Ω´÷∏’ÎÀ˘¬‰…»–Œ÷–µƒ2∏ˆ ˝◊÷∑÷±◊˜Œ™∆Ω√Ê÷±Ω«◊¯±Íœµ÷–“ª∏ˆµ„µƒ∫·◊¯±Í°¢◊ð◊¯±Í£Æ
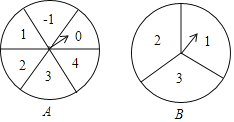
£®1£©”√±Ì∏Ò¡–≥ˆ’‚—˘µƒµ„À˘”–ø…ƒÐµƒ◊¯±Í£ª
£®2£©«Û’‚–©µ„¬‰‘⁄∂˛¥Œ∫Ø ˝y£Ωx2©Å5x+6µƒÕºœÛ…œµƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“√«‘º∂®£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–¡ΩÃı≈◊ŒÔœþ”–«“÷ª”–“ª∏ˆΩªµ„ ±£¨Œ“√«≥∆’‚¡ΩÃı≈◊ŒÔœþŒ™°∞ø§‘∞«£ ÷≈◊ŒÔœþ°±£¨’‚∏ˆΩªµ„Œ™°∞ø§‘∞µ„°±£Æ¿˝»Á£∫≈◊ŒÔœþ![]() ”Î
”Î![]() «°∞ø§‘∞«£ ÷≈◊ŒÔœþ°±£¨°∞ø§‘∞µ„°±Œ™
«°∞ø§‘∞«£ ÷≈◊ŒÔœþ°±£¨°∞ø§‘∞µ„°±Œ™![]() £Æ
£Æ
£®1£©»ÁÕº£¨»Ù≈◊ŒÔœþ![]() ”Î
”Î![]() Œ™°∞ø§‘∞«£ ÷≈◊ŒÔœþ°±£¨«Û
Œ™°∞ø§‘∞«£ ÷≈◊ŒÔœþ°±£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©‘⁄£®1£©µƒÃıº˛œ¬£¨»Ùµ„![]() «µ⁄“ªœÛœÞƒ⁄≈◊ŒÔœþ
«µ⁄“ªœÛœÞƒ⁄≈◊ŒÔœþ![]() …œµƒ∂ص„£¨π˝
…œµƒ∂ص„£¨π˝![]() ◊˜
◊˜![]() ÷·£¨
÷·£¨![]() Œ™¥π◊„£¨«Û
Œ™¥π◊„£¨«Û![]() µƒ◊Ó¥Û÷µ£ª
µƒ◊Ó¥Û÷µ£ª
£®3£©‘⁄£®1£©µƒÃıº˛œ¬£¨…˵„![]() «≈◊ŒÔœþ
«≈◊ŒÔœþ![]() ”Î
”Î![]() µƒ°∞ø§‘∞µ„°±£¨µ„
µƒ°∞ø§‘∞µ„°±£¨µ„![]() «≈◊ŒÔœþ
«≈◊ŒÔœþ![]() …œ“ª∂ص„£¨Œ ‘⁄≈◊ŒÔœþ
…œ“ª∂ص„£¨Œ ‘⁄≈◊ŒÔœþ![]() µƒ∂‘≥∆÷·…œ «∑ҥʑ⁄µ„
µƒ∂‘≥∆÷·…œ «∑ҥʑ⁄µ„![]() £¨ π
£¨ π![]() «“‘µ„
«“‘µ„![]() Œ™÷±Ω«∂•µ„µƒµ»—¸÷±Ω«»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„
Œ™÷±Ω«∂•µ„µƒµ»—¸÷±Ω«»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
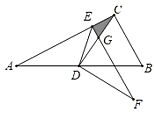
°æƒø°ø»ÁÕº£¨![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() «
«![]() µƒ÷–œþ£¨
µƒ÷–œþ£¨![]() «
«![]() …œ“ª∂ص„£¨Ω´
…œ“ª∂ص„£¨Ω´![]() —ÿ
—ÿ![]() ’€µ˛£¨µ„
’€µ˛£¨µ„![]() ¬‰‘⁄µ„
¬‰‘⁄µ„![]() ¥¶£¨
¥¶£¨![]() ”Îœþ∂Œ
”Îœþ∂Œ![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨»Ù
£¨»Ù![]() «÷±Ω«»˝Ω«–Œ£¨‘Ú
«÷±Ω«»˝Ω«–Œ£¨‘Ú![]() _____£Æ
_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
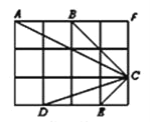
°æƒø°ø»ÁÕº£¨‘⁄![]() µƒ’˝∑Ω–Œ∑Ω∏Ò÷–£¨
µƒ’˝∑Ω–Œ∑Ω∏Ò÷–£¨![]() ∫Õ
∫Õ![]() µƒ∂•µ„∂º‘⁄±þ≥§Œ™1µƒ–°’˝∑Ω–Œµƒ∂•µ„…œ£Æ
µƒ∂•µ„∂º‘⁄±þ≥§Œ™1µƒ–°’˝∑Ω–Œµƒ∂•µ„…œ£Æ
£®1£©ÃÓø’£∫![]() £¨
£¨![]() £ª
£ª
£®2£©≈–∂œ![]() ”Î
”Î![]() «∑ÒœýÀ∆£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
«∑ÒœýÀ∆£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com