练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

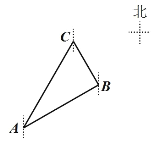
    【题目】在一次夏令营中，小亮从位于点的营地出发，沿北偏东60°方向走了到达地，然后再沿北偏西30°方向走了若干千米到达地，测得地在地南偏西30°方向，则、两地的距离为_________．

    【答案】

    【解析】

    由已知可得到△ABC是直角三角形，从而根据三角函数即可求得AC的长．

    解：如图．由题意可知，AB=5km，∠2=30°，∠EAB=60°，∠3=30°．

    ∵EF//PQ，
    ∴∠1=∠EAB=60°
    又∵∠2=30°，
    ∴∠ABC=180°∠1∠2=180°60°30°=90°，
    ∴△ABC是直角三角形．
    又∵MN//PQ，
    ∴∠4=∠2=30°．
    ∴∠ACB=∠4+∠3=30°+30°=60°．
    ∴AC= = = (km)，
    故答案为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加元，每天售出件．

    （1）请写出与之间的函数表达式；

    （2）当为多少时，超市每天销售这种玩具可获利润2250元？

    （3）设超市每天销售这种玩具可获利元，当为多少时最大，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形的边长为，点为边上一点，，点为的中点，过点作直线分别与，相交于点，.若，则长为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

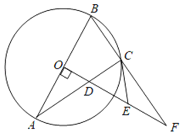
    【题目】如图，△ABC内接于⊙O，AB为直径，作OD⊥AB交AC于点D，延长BC，OD交于点F，过点C作⊙O的切线CE，交OF于点E．

    （1）求证：EC＝ED；

    （2）如果OA＝4，EF＝3，求弦AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

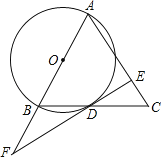
    【题目】如图，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D，过点D作⊙O的切线DE交AC于点E，交AB延长线于点F．

    （1）求证：DE⊥AC；

    （2）若AB＝10，BF＝，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

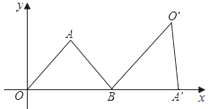
    【题目】如图，△AOB为等腰三角形，顶点A的坐标（2，），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（　　）

    A. （，） B. （，） C. （，） D. （，4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，二次函数y=x2+2x﹣3的图象如图所示，点A（x1，y1），B（x2，y2）是该二次函数图象上的两点，其中﹣3≤x1＜x2≤0，则下列结论正确的是（　　）

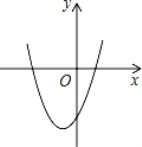
    A. y1＜y2B．y1＞y2C．y的最小值是﹣3 D．y的最小值是﹣4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BC＞AB＞AC．甲、乙两人想在BC上取一点P，使得∠APC＝2∠ABC，其作法如下：

    （甲）作AB的中垂线，交BC于P点，则P即为所求；

    （乙）以B为圆心，AB长为半径画弧，交BC于P点，则P即为所求．

    对于两人的作法，下列判断何者正确？（　　）

    A. 两人皆正确B. 两人皆错误C. 甲正确，乙错误D. 甲错误，乙正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于某一函数给出如下定义：对于任意实数，当自变量时，函数关于的函数图象为，将沿直线翻折后得到的函数图象为，函数的图象由和两部分共同组成，则函数为原函数的“对折函数”，如函数()的对折函数为.

    (1)求函数()的对折函数；

    (2)若点在函数()的对折函数的图象上，求的值；

    (3)当函数()的对折函数与轴有不同的交点个数时，直接写出的取值范围.

    查看答案和解析>>

    同步练习册答案